题目内容
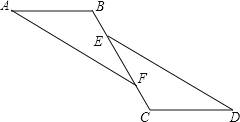
【题目】如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF(____________________________)
即:___________
∵AB∥CD
∴∠B=∠C(_________________________)
在△ABF和△DCE中,
∠A=∠D, ∠B=∠C, BF=CE
∴△ABF≌△DCE(________)
∴∠AFB=∠DEC(_________________________________)
∴AF∥ED(__________________________________)
【答案】等式的性质BF=CE两直线平行内错角相等AAS全等三角形对应角相等内错角相等两直线平行
【解析】
由BE= CF,利用等式的性质得到BF= CE ,再由AB与DC平行得到两对内错角相等,利用AAS得到△ABF与△DCE全等,利用全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
证明:∵BE=FC
∴BE+EF=FC+EF( 等式的性质 )
即: BF=CE
∵AB∥CD
∴∠B=∠C( 两直线平行内错角相等 )
∠A=∠D
∠B=∠C
在△ABF和△DCE中,有
BF=CE
∴△ABF≌△DCE( AAS )
∴∠AFB=∠DEC( 全等三角形对应角相等 )
∴AF∥ED( 内错角相等两直线平行 )

练习册系列答案
相关题目