题目内容
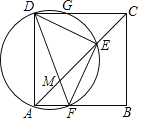
【题目】(1)已知等边△ABC内接于⊙O.点P为![]() 上的一个动点,连结PA、PB、PC.
上的一个动点,连结PA、PB、PC.
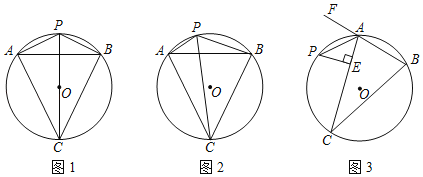
①如图1,当线段PC经过点O时,试写出线段PA,PB,PC之间满足的等量关系,并说明理由;
②如图2,点P为![]() 上的任意一点(点P不与点A、点B重合),试探究线段PA,PB,PC之间满足的等量关系,并证明你的结论;
上的任意一点(点P不与点A、点B重合),试探究线段PA,PB,PC之间满足的等量关系,并证明你的结论;
(2)如图3,在△ABC中,AB=4,AC=7,∠BAC的外角平分线交△ABC的外接圆于点P,PE⊥AC于E,求AE的长.
【答案】(1)①PA+PB=PC,理由详见解析;②PA+PB=PC,理由详见解析;(2)AE=![]() .
.
【解析】
(1)由圆周角定理得出∠PAC=∠PBC=90°,由等边三角形的性质得出∠ABC=∠BAC=60°,求出∠ACP=∠BCP=30°,由直角三角形的性质得出PA=![]() PC,PB=
PC,PB=![]() PC,即可得出结论;
PC,即可得出结论;
②在PC上截取PD=PA,连接AD,证明△APD是等边三角形,得出AD=AP=PD,∠PAD=60°=∠BAC,证出∠DAC=∠PAB,证明△ACD≌△ABP(SAS),得出DC=PB,即可得出结论;
(2)在AC上截取ED=AE.连接PD并延长交圆O于G.连接CG,由线段垂直平分线的性质得出PA=PD,由等腰三角形的性质和圆周角定理得出得出∠PAD=∠PDA=∠CDG.∠PAD=∠G.得出∠CDG=∠G,证出CG=CD,证出∠BAC=180°﹣2∠PAD=180°﹣(∠PAD+∠PDA)=∠APG.得出![]() ,得出
,得出![]() ,证出AB=CG.即可得出答案.
,证出AB=CG.即可得出答案.
解:(1)①![]() ,理由如下:
,理由如下:
![]() 线段
线段![]() 经过点
经过点![]() ,
,
![]() 是
是![]() 的直径,
的直径,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
②![]() ,理由如下:
,理由如下:
在![]() 上截取
上截取![]() ,连接
,连接![]() ,如图2所示:
,如图2所示:
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,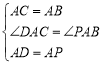 ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)在![]() 上截取
上截取![]() .连接
.连接![]() 并延长交圆
并延长交圆![]() 于
于![]() .连接
.连接![]() ,如图3所示:
,如图3所示:
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() ,
,
又![]() 平分
平分![]() ,
,
![]() .
.
![]()
![]()
![]()
![]() ,
,
![]() .
.
![]() ,即
,即![]() ,
,
![]() .
.