题目内容
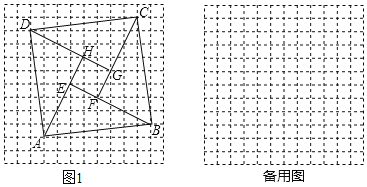
【题目】如图示，在
中，
，
，
，点
在内部，且
，连接
，则的最小值等于______.
【答案】
【解析】
首先判定直角三角形∠CAB=30°，∠ABC=60°，
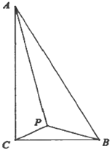
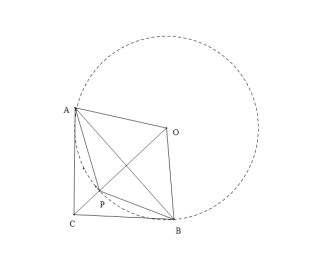
，然后根据
，得出∠ACB+∠PAC+∠PBC=∠APB=120°，定角定弦，点P的轨迹是以AB为弦，圆周角为120°的圆弧上，如图所示，当点C、O、P在同一直线上时，CP最小，构建圆，利用勾股定理，即可得解.
∵
，
，
，
∴
∴∠CAB=30°，∠ABC=60°
∵，∠PAB+∠PAC=30°
∴∠ACB+∠PAC+∠PBC=∠APB=120°
∴定角定弦，点P的轨迹是以AB为弦，圆周角为120°的圆弧上，如图所示，当点C、O、P在同一直线上时，CP最小
∴CO⊥AB，∠COB=60°，∠ABO=30°
∴OB=2，∠OBC=90°
∴
∴
故答案为.
练习册系列答案
冲刺100分1号卷系列答案
相关题目
