Question

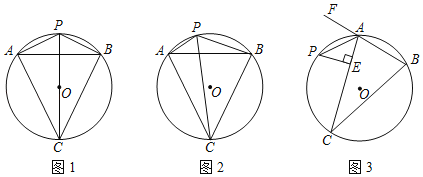
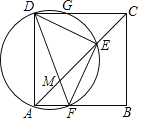
【题目】如图，已知在正方形ABCD中，连结AC，在AC上截取AE＝AD，作△ADE的外接圆交AB于点F，连结DF交AC于点M，连结EF，下列选项不正确的是（　　）

A.

B.AM＝EC

C.∠EFB＝∠AFD

D.S四边形BCMF＝S四边形ADEF

Answer 1

【答案】D

【解析】

连接FG，根据正方形的性质得到∠DAF＝∠ADC＝90°，由圆周角定理得到∠DGF＝90°，推出四边形AFGD是矩形，得到DG＝AF，求得＝，故A正确；根据等腰三角形的性质得到∠ADE＝∠AED，等量代换得到∠EFB＝∠AFD，故C正确；推出△DEF是等腰直角三角形，得到DE＝EF，根据全等三角形的性质得到∠AEF=∠ADF=∠CDE，再证明△ADM≌△CDE即可得到，故B正确；连接BE，求得S四边形ADEF＝S△ADE+S△AEF＝S△ADE+S△CDE＝S△ACD＝S△ABC，由于S四边形BCMF＜S△ABC，得到S四边形BCMF＜S四边形ADEF，故D错误．

解：连接FG，

∵四边形ABCD是正方形，

∴∠DAF＝∠ADC＝90°，

∴DF是圆的直径，

∴∠DGF＝90°，

∴四边形AFGD是矩形，

∴DG＝AF，

∴＝，故A正确；

∵AD＝AE，

∴∠ADE＝∠AED，

∵∠AFD＝∠AED，∠BFE＝∠ADE，

∴∠EFB＝∠AFD，故C正确；

∵DF是圆的直径，

∴∠DEF＝90°，

∵∠DFE＝∠DAC＝45°，

∴△DEF是等腰直角三角形，

∴DE＝EF，

∵∠CDE+∠ADE＝∠AEF+∠AED＝90°，

∴∠CDE＝∠EAF，

∴△CDE≌△AEF（SAS），

∴∠AEF=∠ADF=∠CDE，

又∵AD=CD，∠DAM=∠ECD=45°，

∴△ADM≌△CDE，

∴AM=CE，故B正确；

连接BE，

∵AE＝BC＝AD，CE＝AF，∠CAF＝∠BCE＝45°，

∴△AEF≌△CBE（SAS），

∴S四边形ADEF＝S△ADE+S△AEF＝S△ADE+S△CDE＝S△ACD＝S△ABC，

∵S四边形BCMF＜S△ABC，

∴S四边形BCMF＜S四边形ADEF，故D错误，

故选：D．