Question

【题目】如图，矩形ABCD中，对角线AC的垂直平分线EF分别交BC，AD于点E，F，若BE=3，AF=5，则AC的长为（ ）

A. B. C. 10D. 8

Answer 1

【答案】A

【解析】

连接AE，由线段垂直平分线的性质得出OA=OC，AE=CE，证明△AOF≌△COE得出AF=CE=5，得出AE=CE=5，BC=BE+CE=8，由勾股定理求出AB=4，再由勾股定理求出AC即可．

解：如图，连结AE，

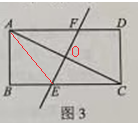
设AC交EF于O，

依题意，有AO＝OC，∠AOF＝∠COE，∠OAF＝∠OCE，

所以，△OAF≌△OCE（ASA），

所以，EC＝AF＝5，

因为EF为线段AC的中垂线，

所以，EA＝EC＝5，

又BE＝3，由勾股定理，得：AB＝4，

所以，AC＝