题目内容
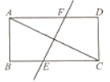
【题目】如图,正方形ABCD中,对角线AC=8cm.射线AF⊥AC,垂足为A.动点P从点C出发在CA上运动,动点Q从点A出发在射线AF上运动,两点的运动速度都是2cm/s.若两点同时出发,多少时间后,四边形AQBP是特殊四边形?请说明特殊四边形的名称及理由.

【答案】当P、Q运动2s后,四边形AQBP是正方形,理由见解析
【解析】
当P、Q运动2s后,四边形AQBP是正方形,由题意可得AQ=AP=BP=4cm,由等腰直角三角形的性质可得BP⊥AC,可得AF∥BP,可证四边形APBQ是平行四边形,且BP⊥AC,AP=BP,可得四边形APBQ是正方形.
解:当P、Q运动2s后,四边形AQBP是正方形,

理由如下:∵四边形ABCD是正方形
∴AB=BC
当P、Q运动2s后,CP=AQ=4cm,
∵AC=8cm,
∴AP=CP=4cm,且AB=BC,
∴BP⊥AC,且AF⊥AC
∴AF∥BP,且AQ=BP=4cm,
∴四边形APBQ是平行四边形,且BP⊥AC,AP=BP
∴四边形AQBP是正方形

练习册系列答案
相关题目