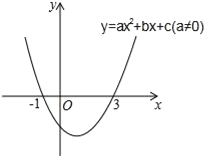题目内容
【题目】如图，抛物线与x轴交于A（x1，0）、B（x2，0）两点，且x1＜x2，与y轴交于点C（0，﹣4），其中x1，x2是方程x2﹣4x﹣12=0的两个根．
（1）求A、B两点坐标；
（2）求抛物线的解析式；
（3）点M是线段AB上的一个动点（不与A、B两点重合），过点M作MN∥BC，交AC于点N，连接CM，在M点运动时，△CMN的面积是否存在最大值？若存在，求出△CMN面积最大时点M的坐标；若不存在，请说明理由．
【答案】（1）A（﹣2，0），B（6，0）．（2）y=
x2﹣
x﹣4．（3）存在，点M的坐标为（2，0）．
【解析】
(1)通过解方程能求出两根,再根据题干给出的大小关系确定A、B点的坐标.
(2)已知A、B、C三点坐标,利用待定系数法即可确定该函数的解析式.
(3)首先设点M的坐标,然后表示出AM的长;已知MN//BC,利用相似三角形三角形AMN、三角形ABC求出三角形AMN的面积表达式;以AM为底、OC为高易得三角形ACM的面积, 三角形ACM、三角形AMN的面积差即为三角形MNC的面积,再根据所得函数的性质来判断三角形MNC是否具有最大面积.
解：（1）∵x2﹣4x﹣12=0，
∴x1=﹣2，x2=6．
即：A（﹣2，0），B（6，0）．
（2）∵抛物线过点A、B、C，
∴设抛物线的解析式为y=a（x+2）（x﹣6），将点C的坐标代入，得：
﹣4=a（0+2）（0﹣6），
解得a=
．
∴抛物线的解析式为y=x2﹣
x﹣4．
（3）存在．
设点M的坐标为（m，0），过点N作NH⊥x轴于点H
∵点A的坐标为（﹣2，0），点B的坐标为（6，0），
∴AB=8，AM=m+2．
∵MN∥BC，∴△AMN∽△ABC．
∴
=
，∴
=
，
∴NH=
∴S△CMN
=S△ACM﹣S△AMN
=
AMCO﹣AMNH
=（m+2）（4﹣）
=﹣
m2+m+3
=﹣（m﹣2）2+4．
∴当m=2时，S△CMN有最大值4．
此时，点M的坐标为（2，0）．
