题目内容
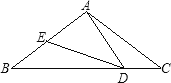
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度向点
的速度向点![]() 运动,设运动时间为
运动,设运动时间为![]() 秒
秒![]() .
.
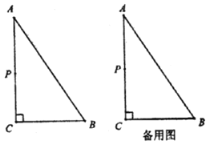
(1)若点![]() 恰好在
恰好在![]() 的角平分线上,求出此时
的角平分线上,求出此时![]() 的值;
的值;
(2)若点![]() 使得
使得![]() 时,求出此时
时,求出此时![]() 的值.
的值.
【答案】(1) 5秒 (2) ![]() 秒
秒
【解析】
(1) 作PD⊥AB于D,依据题意求出![]() ∽
∽ ![]() ,设AP为x,用x表示PC,求出x即可.
,设AP为x,用x表示PC,求出x即可.
(2)当P在AC上时,作PD⊥AB于D,由题意可得△ABP为等腰三角形PD也是中线,求出AD,根据![]() ∽
∽![]() ,求出AP即可求出时间t.
,求出AP即可求出时间t.
(1)如图,作PD⊥AB于D,
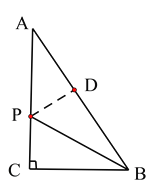
∵点![]() 恰好在
恰好在![]() 的角平分线上
的角平分线上
∴PC=PD
∵![]()
![]()
∴![]() ∽
∽ ![]()
∴![]()
∵![]()
![]()
∴![]()
设AP为x,PC=![]()
根据勾股定理得到 ![]()
![]()
解得:x=5
∴AP=5
∴t![]() =5 秒
=5 秒
答:若点![]() 恰好在
恰好在![]() 的角平分线上,t为5秒.
的角平分线上,t为5秒.
(2)作PD⊥AB于D,
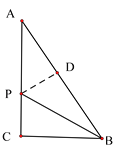
∵ PB+PC=AC
∴ A=PB
∴AD=BD=5
∵∠A=∠A ∠ADP=∠ACB
∴![]() ∽
∽![]()
∴![]()
∵ ![]() ,
,![]()
∴![]()
∴t=![]() 秒
秒
答:![]() 为
为![]() 秒.
秒.

练习册系列答案
相关题目