题目内容
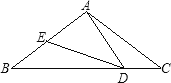
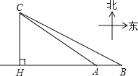
【题目】如图，在一笔直的海岸线上有
、
两个观测站，在的正东方向，
千米，在某一时刻，从观测站测得一艘集装箱货船位于北偏西
的
处，同时观测站测得改集装箱船位于北偏西
方向，问此时该集装箱船与海岸之间距离
约多少千米？（最后结果保留整数）
（参考数据：
，
，
，
，
，
）
【答案】此时该集装箱船与海岸之间距离
约
千米．
【解析】
设CH=x，在直角△ABC中利用三角函数和x，表示出AH的长，同理在直角△BHC中，利用x表示出BH，根据AB=10，即BH﹣AH=10，即可列方程求得CH的长．
设CH=x，在直角△ABC中，∠ACH=62.6°．
∵tan∠ACH=
，∴AH=xtan62.6°，在直角△BHC中，∠BCH=69.2°．
∵tan∠BCH=
，∴BH=xtan69.2°．
∵AB=BH﹣AH，∴xtan69.2°﹣xtan62.6°=10，解得：x=
≈14．
答：此时该集装箱船与海岸之间距离CH约14千米．
练习册系列答案
名校课堂系列答案
相关题目
【题目】光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台，先将这50台联合收割机派往A、B两地区收割小麦，其中30台派往A地区，20台派往B地区．两地区与该农机租赁公司商定的每天的租赁价格见表：
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
（1）设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y（元），求y与x间的函数关系式，并写出x的取值范围；
（2）若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元，说明有多少种分配方案，并将各种方案设计出来；
（3）如果要使这50台联合收割机每天获得的租金最高，请你为光华农机租赁公司提一条合理化建议．
