Question

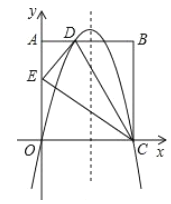
【题目】在平面直角坐标系xOy中，点A（t，0），B（t+2，0），C（n，1），若射线OC上存在点P，使得△ABP是以AB为腰的等腰三角形，就称点P为线段AB关于射线OC的等腰点．

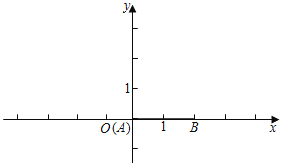
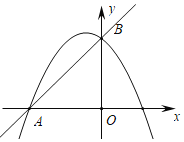
（1）如图，t＝0，

①若n＝0，则线段AB关于射线OC的等腰点的坐标是　 　；

②若n＜0，且线段AB关于射线OC的等腰点的纵坐标小于1，求n的取值范围；

（2）若n＝，且射线OC上只存在一个线段AB关于射线OC的等腰点，则t的取值范围是　 　．

Answer 1

【答案】（1）①（0,2） ② （2）﹣4＜t≤﹣2或t＝0或﹣2＜t≤

【解析】

（1）①根据线段AB关于射线OC的等腰点的定义可知OP＝AB＝2，由此即可解决问题．

②如图2中，当OP＝AB时，作PH⊥x轴于H．求出点P的横坐标，利用图象法即可解决问题．

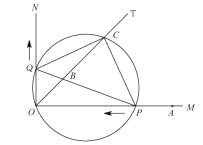
（2）如图3﹣1中，作CH⊥y轴于H．分别以A，B为圆心，AB为半径作⊙A，⊙B．首先证明∠COH＝30°，由射线OC上只存在一个线段AB关于射线OC的等腰点，推出射线OC与⊙A，⊙B只有一个交点，求出几种特殊位置t的值，利用数形结合的思想解决问题即可．

解：（1）①如图1中，由题意A（0，0），B（2，0），C（0，1），

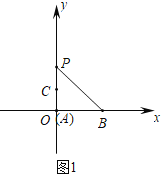
∵点P是线段AB关于射线OC的等腰点，

∴OP＝AB＝2，

∴P（0，2）．

故答案为（0，2）．

②如图2中，当OP＝AB时，作PH⊥x轴于H．

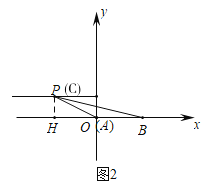
在Rt△POH中，∵PH＝OC＝1，OP＝AB＝2

∴OH＝＝，

观察图象可知：若n＜0，且线段AB关于射线OC的等腰点的纵坐标小于1时，n＜﹣．

（2）如图3﹣1中，作CH⊥y轴于H．分别以A，B为圆心，AB为半径作⊙A，⊙B．

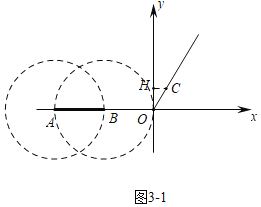
由题意C（，1），

∴CH＝，OH＝1，

∴tan∠COH＝＝，

∴∠COH＝30°，

当⊙B经过原点时，B（﹣2，0），此时t＝﹣4，

∵射线OC上只存在一个线段AB关于射线OC的等腰点，

∴射线OC与⊙A，⊙B只有一个交点，观察图象可知当﹣4＜t≤﹣2时，满足条件，

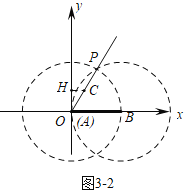
如图3﹣2中，当点A在原点时，∵∠POB＝60°，此时两圆的交点P在射线OC上，满足条件，此时t＝0，

如图3﹣3中，当⊙B与OC相切于P时，连接BP．

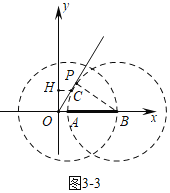
∴OC是⊙B的切线，

∴OP⊥BP，

∴∠OPB＝90°，

∵BP＝2，∠POB＝60°，

∴OB＝＝，此时t＝﹣2，

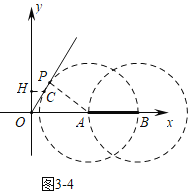
如图3﹣4中，当⊙A与OC相切时，同法可得OA＝，此时t＝

观察图形可知，满足条件的t的值为：﹣2＜t≤，

综上所述，满足条件t的值为﹣4＜t≤﹣2或t＝0或﹣2＜t≤．

故答案为：﹣4＜t≤﹣2或t＝0或﹣2＜t≤．