题目内容
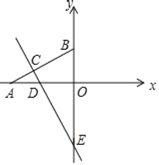
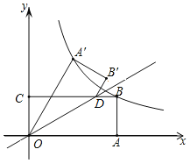
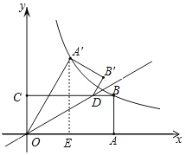
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=![]() (k≠0)的图象恰好经过点A′,B,则k的值为______.
(k≠0)的图象恰好经过点A′,B,则k的值为______.
【答案】![]()
【解析】
设B(m,1),得到OA=BC=m,根据轴对称的性质得到OA′=OA=m,∠A′OD=∠AOD=30°,求得∠A′OA=60°,过A′作A′E⊥OA于E,解直角三角形得到A′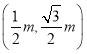 ,将A′,B的坐标代入反比例函数解析式得出关于m的方程即可求解.
,将A′,B的坐标代入反比例函数解析式得出关于m的方程即可求解.
解:∵四边形ABCO是矩形,AB=1,
∴设B(m,1),
∴OA=BC=m,
∵四边形OA′B′D与四边形OABD关于直线OD对称,
∴OA′=OA=m,∠A′OD=∠AOD=30°,
∴∠A′OA=60°,
过A′作A′E⊥OA于E,
![]() ,
,
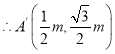 ,
,
∵反比例函数y=![]() (k≠0)的图象恰好经过点A′,B,
(k≠0)的图象恰好经过点A′,B,
![]() ,
,![]() ,
,
即点B的坐标为(1,![]() ),
),![]() .
.
故答案为:![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
【题目】成都市某公司自主设计了一款可控温杯,每个生产成本为16元,投放市场进行了试销.经过调查得到每月销售量y(万个)与销售单价x(元/个)之间关系是一次函数的关系,部分数据如下:
销售单价x(元/个) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万个) | … | 60 | 50 | 40 | 30 | … |
(1)求y与x之间的函数关系;
(2)该公司既要获得一定利润,又要符合相关部门规定(一件产品的利润率不得高于50%)请你帮助分析,公司销售单价定为多少时可获利最大?并求出最大利润.