题目内容
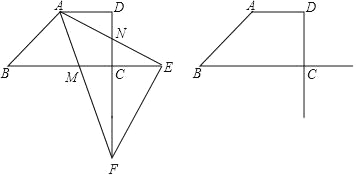
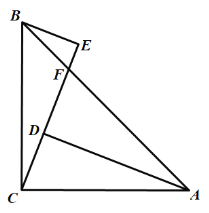
【题目】如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F.
(1)求证:△CEB≌△ADC;
(2)若AD=9cm,DE=6cm,求BE及EF的长.
【答案】(1)见解析;(2)BE=3 cm,EF=![]() cm.
cm.
【解析】
(1)由同角的余角相等可得∠BCE=∠CAD,而BC=AC,∠E=∠CDA=90°,故有△CEB≌△ADC;(2)由(1)知BE=DC,CE=AD,有CE=AD=9,DC=CE-DE=3,BE=DC=3,可证得△BFE∽△AFD,有![]() 故可求得EF的值.
故可求得EF的值.
(1)证明:∵BE⊥CE于E,AD⊥CE于D,∠ACB=90°,
∴∠E=∠ADC=90°,∠BCE=90°-∠ACD,∠CAD=90°-∠ACD,
∴∠BCE=∠CAD
在△BCE与△CAD中,
∠E=∠ADC,∠BCE=∠CAD,BC=AC
∴△CEB≌△ADC(AAS)
(2)∵△CEB≌△ADC,
∴BE=DC,CE=AD,
又∵AD=9
∴CE=AD=9,DC=CE-DE=9-6=3,
∴BE=DC=3(cm),
∵∠E=∠ADF=90°,∠BFE=∠AFD,
∴△BFE∽△AFD,
∴![]() ,即有
,即有![]() 解得:EF=
解得:EF=![]() (cm).
(cm).
∴BE=3cm,EF=![]() cm.
cm.

练习册系列答案
相关题目