题目内容
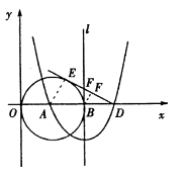
【题目】如图，已知点A（3，0），以A为圆心作⊙A与Y轴切于原点，与x轴的另一个交点为B，过B作⊙A的切线l．
（1）以直线l为对称轴的抛物线过点A及点C（0，9），求此抛物线的解析式；
（2）抛物线与x轴的另一个交点为D，过D作⊙A的切线DE，E为切点，求DE的长；
（3）点F是切线DE上的一个动点，当△BFD与△EAD相似时，求出BF的长 ．
【答案】
（1）解：由题意可知，抛物线的对称轴为直线x=6，
∴设抛物线的解析式为y=a （x-6）2+k，
∵抛物线经过点A（3，0）和C（0，9），
∴将A，C两点坐标代入得： 
，解得：a= 
，k=-3．
∴抛物线的解析式为y= （x-6）2-3
（2）解：连接AE，
∵DE是⊙A的切线，
∴∠AED=90°，AE=3 ，
∵直线l是抛物线的对称轴，点A，D是抛物线与x轴的交点，
∴AB=BD=3，
∴AD=6 ， 在Rt△ADE中，DE2=AD2-AE2=62-32=27，
∴DE=3 
（3）解：利用有两个角对应相等的两个三角形相似，
当BF⊥ED时，∵∠AED=∠BFD=90°，∠ADE=∠BDF，
∴△AED∽△BFD，∴ 
，即 
，
∴BF= 
．
当FB⊥AD时，∵∠AED=∠FBD=90°，∠ADE=∠FDB，
∴△AED∽△FBD ，
∴ 
即BF= 
，
∴当△BFD与△EAD相似时，BF的长为 或 ．
【解析】（1）根据题意可知此抛物线的对称轴为x=6，设抛物线的解析式为顶点式，再将点A、C两点坐标代入解析式，建立方程求解，即可求出此函数解析式。
（2） 由DE是⊙A的切线，因此添加辅助线连接AE，得出∠AED=90°，AE=3 ，再根据圆的对称性及抛物线的对称性，求出AD的长， 在Rt△ADE中，利用勾股定理求出DE的长。
（3）抓住已知点F是切线DE上的一个动点，要使△BFD与△EAD相似，图形中隐含公共角∠ADE=∠BDF，因此分两种情况：当BF⊥ED时；当FB⊥AD时，根据相似三角形的性质，得出对应边成比例，建立方程，即可求出BF的长。
