题目内容
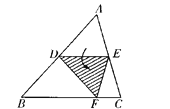
【题目】如图，点D为边AB的中点，DE∥BC，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=50°，则∠EDF=_______，∠BDF=_______，若AB=10cm，则FD= ________cm。
【答案】50°80°5
【解析】
根据过三角形一边的中点且平行于另一边的直线必平分第三边可得E是AC的中点，进而得到DE是△ABC的中位线，DE∥BC,再根据两直线平行,同位角相等可得∠ADE=∠B ,根据翻折变换的性质可得∠ADE=∠EDF ,然后根据平角等于180°列式计算即可得解;根据线段中点的定义求出AD,再根据翻折的性质可得FD=AD.
点D为边AB的中点, DE∥BC，
∴E是AC的中点,
∴DE是△ABC的中位线,
∵DE∥BC,
∴∠ADE=∠B=50°,
由翻折的性质得, ∠ADE=∠EDF=50°,
∴∠BDF=180°-∠ADE-∠EDF=180°-50°-50°=80°,
∵AB=10cm,点D是AB的中点,
∴AD=
AB=×10=5cm,
由翻折的性质得,FD=AD=5cm.
故答案为:50°,80°,5.
练习册系列答案
相关题目
