题目内容
【题目】如图，在正方形ABCD中，将正方形的边AD绕点A顺时针旋转到AE，连接BE、DE，过点A作AF⊥BE于F，交直线DE于P．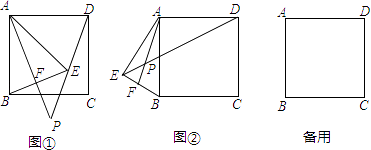
（1）如图①，若∠DAE=40°，求∠P的度数；
（2）如图②，若90°＜∠DAE＜180°，其它条件不变，试探究线段AP、DP、EP之间的数量关系，并说明理由；
（3）继续旋转线段AD，若旋转角180°＜∠DAE＜270°，则线段AP、DP、EP之间的数量关系为（直接写出结果）
【答案】
（1）
解：∵四边形ABCD是正方形，
∴AD=AB，∠BAD=90°，
∵AD绕点A顺时针旋转到AE，
∴AD=AE，
∵∠DAE=40°，
∴∠ADE=∠AED=70°，∠BAE=50°，
∵AF⊥BE，
∴∠FAE=∠FAB=25°，
∴∠P=∠AED﹣∠PAE=45°；
（2）
解：如图2，过A作AQ⊥DE于Q，
则∠PAQ=∠BAQ+∠FAB，
∵AE=AB，AF⊥BE，
∴∠FAE=∠BAF，
∴∠APQ=∠EAF+∠AEP，
∵∠BAD=∠AQP=90°，
∴∠BAQ=∠ADQ，
∵AE=AD，
∴∠ADQ=∠AEP，
∴∠BAQ=∠AEP，
∴∠APQ=∠PAQ=45°，
∴PQ= 
AP，
∴PE+PQ=PD﹣PQ，
即PE+ AP=PD﹣ AP，
∴PD= 
AP+PE；
（3）PE=PD+ PA
【解析】解：（3）如图3，过A作AQ⊥DE于Q，则∠AQP=90°，
∵AD=AE，
∴DQ=EQ，∠AEQ=∠ADQ，
∵AE=AB，AF⊥BE，
∴∠3=∠FAB，
∵∠APQ=∠3﹣∠AEQ=∠3﹣∠ADQ，
∵∠1+∠FAB=∠FAB+∠ABF=90°，
∴∠1=∠ABF=∠AEF，
∴∠2=90°﹣∠1﹣∠ADP=90°﹣（90°﹣∠3）﹣∠AEP=∠3﹣∠AEP，
∴∠2=∠APQ=45°，
∴PQ= AP，
∴PD+PQ=PE﹣PQ，
即PD+ PA=PE﹣ PA，
∴PE=PD+ PA．
所以答案是：PE=PD+ PA．
【考点精析】通过灵活运用等腰三角形的性质，掌握等腰三角形的两个底角相等（简称：等边对等角）即可以解答此题．
