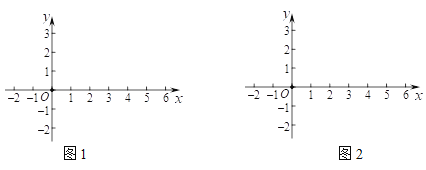题目内容
【题目】在△ABC中,CD是△ABC的中线,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中线弧.
为△ABC的中线弧.
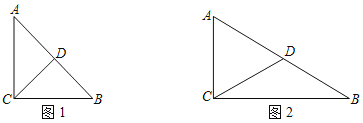
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点.
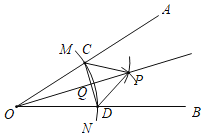
①如图1,若∠A=45°,画出△ABC的一条中线弧![]() ,直接写出△ABC的中线弧
,直接写出△ABC的中线弧![]() 所在圆的半径r的最小值;
所在圆的半径r的最小值;
②如图2,若∠A=60°,求出△ABC的最长的中线弧![]() 的弧长l.
的弧长l.
(2)在平面直角坐标系中,已知点A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中点.求△ABC的中线弧![]() 所在圆的圆心P的纵坐标t的取值范围.
所在圆的圆心P的纵坐标t的取值范围.
【答案】(1)①图见解析,![]() ,②
,②![]() ;(2)t≥5或t≤﹣
;(2)t≥5或t≤﹣![]()
【解析】
(1)①如图1中,当中线弧![]() 的圆心是AC或BC的中点时,
的圆心是AC或BC的中点时,![]() 所在圆的半径r的最小.
所在圆的半径r的最小.
②如图2中,当中线弧![]() 所在的圆与AC,AB都相切时,
所在的圆与AC,AB都相切时,![]() 的弧长最大.
的弧长最大.
(2)分两种情形:如图3中,若中线弧在 线段CD的下方时,如图4中,若中线弧![]() 在 线段CD的上方时,分别求解即可解决问题.
在 线段CD的上方时,分别求解即可解决问题.
解:(1)①如图1中,当直线弧![]() 的圆心是AC或BC的中点时,
的圆心是AC或BC的中点时,![]() 所在圆的半径r的最小,
所在圆的半径r的最小,

当∠A=45°,
此时r=![]() AC=
AC=![]() ,
,
∴△ABC的中线弧![]() 所在圆的半径r的最小值为
所在圆的半径r的最小值为![]() .
.
②如图2中,当中线弧![]() 所在的圆与AC,AB都相切时,
所在的圆与AC,AB都相切时,![]() 的弧长最大,
的弧长最大,
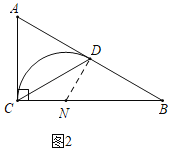
此时,![]() 的圆心在BC上,
的圆心在BC上,
∵ND⊥BD,
∴∠NDB=90°,
∵∠A=60°,∠ACB=90°,
∴∠B=30°,
∴BN=2DN=2CN,
∴3CN=BC=![]() ,
,
∴CN=![]() ,
,
∴半径为![]() .
.
∴△ABC的最长的中线弧![]() 的弧长l
的弧长l![]() ;
;
(2)如图3中,若中线弧![]() 在 线段CD的下方时,
在 线段CD的下方时,
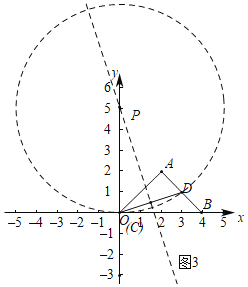
∵△ABC的中线弧![]() 所在的圆的圆心在线段CD使得垂直平分线上,
所在的圆的圆心在线段CD使得垂直平分线上,
当中线弧![]() 所在圆与BC相切时,可得P(0,5),
所在圆与BC相切时,可得P(0,5),
观察图象可知中线弧![]() 所在圆的圆心P的纵坐标t≥5.
所在圆的圆心P的纵坐标t≥5.
如图4中,若中线弧![]() 在 线段CD的上方时,
在 线段CD的上方时,
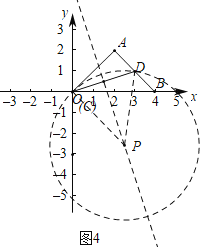
当中线弧![]() 所在圆与AC相切时,可得P(
所在圆与AC相切时,可得P(![]() ,﹣
,﹣![]() ),
),
观察图象可知中线弧![]() 所在圆的圆心P的纵坐标t≤﹣
所在圆的圆心P的纵坐标t≤﹣![]() .
.
综上所述,中线弧![]() 所在圆的圆心P的纵坐标t的取值范围为:t≥5或t≤﹣
所在圆的圆心P的纵坐标t的取值范围为:t≥5或t≤﹣![]() .
.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案【题目】甲、乙两家商场平时以同样的价格出售相同的商品.“五一”节期间两家商场都让利酬宾.在甲商场按累计购物金额的![]() 收费;在乙商场累计购物金额超过
收费;在乙商场累计购物金额超过![]() 元后,超出
元后,超出![]() 元的部分按
元的部分按![]() 收费.设小红在同一商场累计购物金额为
收费.设小红在同一商场累计购物金额为![]() 元,其中
元,其中![]() .
.
(1)根据题意,填写下表(单位:元):
累计购物金额 |
|
|
| ··· |
在甲商场实际花费 |
| ··· | ||
在乙商场实际花费 |
| ··· |
(2)设小红在甲商场实际花费![]() 元,在乙商场实际花费
元,在乙商场实际花费![]() 元,分别求
元,分别求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)“五一”节期间小红如何选择这两家商场去购物更省钱?
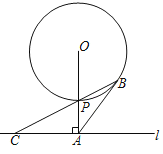
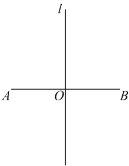
【题目】已知:如图,线段AB=5cm,∠BAM=90°,P是![]() 与∠BAM所围成的图形的外部的一定点,C是
与∠BAM所围成的图形的外部的一定点,C是![]() 上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0.00 | 1.00 | 1.56 | 1.98 | 2.50 | 3.38 | 4.00 | 4.40 | 5.00 |
y1/cm | 2.75 | 3.24 | 3.61 | 3.92 | 4.32 | 5.06 | 5.60 | 5.95 | 6.50 |
y2/cm | 2.75 | 4.74 | 5.34 | 5.66 | 5.94 | 6.24 | 6.37 | 6.43 | 6.50 |
(1)在同一平面直角坐标系xOy中,画出各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(2)连接BP,结合函数图象,解决问题:当△BDP为等腰三角形时,x的值约为_____cm(结果保留一位小数).