题目内容
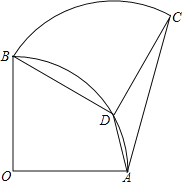
【题目】已知锐角∠AOB,如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
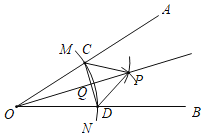
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
【答案】A
【解析】
由作图知OC=OD,CD=CP=DP,根据等边三角形的判定和性质、线段垂直平分线的性质和判定、角平分线的基本作图,逐一判断可得.
由作图可知:射线OP即为∠AOB的角平分线,
∴∠AOP=∠BOP,
故C正确,不符合题意;
由作图(1)(2)可知:OC=OD,CP=DP,
∴OP是CD的垂直平分线,
∴CD⊥OP,
故D正确,不符合题意;
由作图(2)可知:CD=CP=PD,
∴△CDP是等边三角形,
∵CD⊥OP,
∴CP=2CQ,
故B正确,不符合题意;
∵∠AOP=∠BOP,
当OC=CP时,∠AOP=∠CPO,
∴∠CPO=∠BOP,
∴CP∥OB,
故A错误,符合题意;
故选:A.

练习册系列答案
相关题目