题目内容
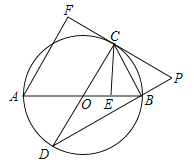
【题目】如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=5.C是直线l上一点,连接CP并延长,交⊙O于点B,且AB=AC.
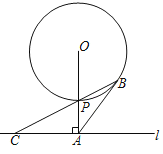
(1)求证:AB是⊙O的切线;
(2)若tan∠ACB=![]() ,求线段BP的长.
,求线段BP的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接OB,由等腰三角形的性质可得∠ACB=∠ABC,∠OBP=∠OPB=∠CPA,由余角的性质可求∠ABO=90°,可得结论;
(2)过点O作OD⊥BP于D,设AP=x,AC=2x,由勾股定理可求AP=2,AC=4,由勾股定理可求CP的长,通过证明△ACP∽△DOP,可求PD的长,由等腰三角形的性质可求BP的长.
证明:(1)连接OB,则OP=OB,

∴∠OBP=∠OPB=∠CPA,
∵AB=AC,
∴∠ACB=∠ABC,
∵OA⊥l,
∴∠OAC=90°,
∴∠ACB+∠CPA=90°,
∴∠ABP+∠OBP=90°,
∴∠ABO=90°,
∴OB⊥AB,
∴AB是⊙O的切线;
(2)如图,过点O作OD⊥BP于D,
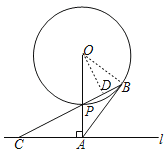
∵tan∠ACB=![]() ,
,
∴设AP=x,AC=2x,
∴AB=2x,OP=OB=5﹣x,
∵AO2=OB2+AB2,
∴25=(5﹣x)2+4x2,
∴x=2,
∴AP=2,AC=4
∴OB=OP=3,
∴CP=![]() ,
,
∵∠CAP=∠ODP=90°,∠APC=∠OPD,
∴△ACP∽△DOP,
∴![]() ,
,
∴PD=![]() ,
,
∵OB=OP,OD⊥BP,
∴BP=2PD=![]() .
.

【题目】疫情期间,甲、乙、丙、丁4名同学约定周一至周五每天做一组俯卧撑.为了增加趣味性,他们通过游戏方式确定每个人每天的训练计划.
首先,按如图方式摆放五张卡片,正面标有不同的数字代表每天做俯卧撑的个数,反面标有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 便于记录.
便于记录.
![]()
具体游戏规则如下:
甲同学:同时翻开![]() ,
,![]() ,将两个数字进行比较,然后由小到大记录在表格中,
,将两个数字进行比较,然后由小到大记录在表格中,![]() ,
,![]() ,
,![]() 按原顺序记录在表格中;
按原顺序记录在表格中;
乙同学:同时翻开![]() ,
,![]() ,
,![]() ,将三个数字进行比较,然后由小到大记录在表格中,
,将三个数字进行比较,然后由小到大记录在表格中,![]() ,
,![]() 按原顺序记录在表格中;
按原顺序记录在表格中;
以此类推,到丁同学时,五张卡片全部翻开,并由小到大记录在表格中.
下表记录的是这四名同学五天的训练计划:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | |
甲同学 |
|
|
|
|
|
乙同学 |
|
|
|
|
|
丙同学 | |||||
丁同学 |
|
|
|
|
|
根据记录结果解决问题:
(1)补全上表中丙同学的训练计划;
(2)已知每名同学每天至少做30个,五天最多做180个.
①如果![]() ,
,![]() ,那么
,那么![]() 所有可能取值为__________________________;
所有可能取值为__________________________;
②这四名同学星期_________做俯卧撑的总个数最多,总个数最多为_________个.
【题目】改革开放以来,人们的支付方式发生了巨大转变,近年来,移动支付已成为主要的支付方式之一,为了解某校学生上个月![]() 两种移动支付方式的使用情况,从全校
两种移动支付方式的使用情况,从全校![]() 名学生中随机抽取了
名学生中随机抽取了![]() 人,发现样本中
人,发现样本中![]() 两种支付方式都不使用的有
两种支付方式都不使用的有![]() 人,样本中仅使用
人,样本中仅使用![]() 种支付方式和仅使用
种支付方式和仅使用![]() 种支付方式的学生的支付金额
种支付方式的学生的支付金额![]() (元)的分布情况如下:
(元)的分布情况如下:
支付金额 支付方式 |
|
|
|
仅使用 |
|
|
|
仅使用 |
|
|
|
下面有四个推断:
①从样本中使用移动支付的学生中随机抽取一名学生,该生使用A支付方式的概率大于他使用B支付方式的概率;
②根据样本数据估计,全校1000名学生中.同时使用A、B两种支付方式的大约有400人;
③样本中仅使用A种支付方式的同学,上个月的支付金额的中位数一定不超过1000元;
④样本中仅使用B种支付方式的同学,上个月的支付金额的平均数一定不低于1000元.其中合理的是( )
A.①③B.②④C.①②③D.①②③④