ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
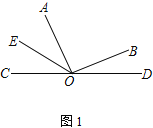
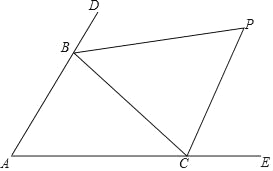
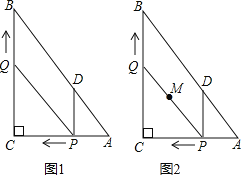
£¬![]() £¬¶ÆµćP“ÓµćAæŖŹ¼ŃŲ±ßACĻņµćCŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£¬¶ÆµćQ“ÓµćCæŖŹ¼ŃŲ±ßCBĻņµćBŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£¬¹żµćP×÷
£¬¶ÆµćP“ÓµćAæŖŹ¼ŃŲ±ßACĻņµćCŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£¬¶ÆµćQ“ÓµćCæŖŹ¼ŃŲ±ßCBĻņµćBŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£¬¹żµćP×÷![]() £¬½»ABÓŚµćD£¬Į¬½ÓPQ£¬µćP”¢Q·Ö±š“ÓµćA”¢CĶ¬Ź±³ö·¢£¬µ±ĘäÖŠŅ»µćµ½“ļ¶ĖµćŹ±£¬ĮķŅ»µćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė
£¬½»ABÓŚµćD£¬Į¬½ÓPQ£¬µćP”¢Q·Ö±š“ÓµćA”¢CĶ¬Ź±³ö·¢£¬µ±ĘäÖŠŅ»µćµ½“ļ¶ĖµćŹ±£¬ĮķŅ»µćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė![]() £®
£®
![]() Ö±½ÓÓĆŗ¬tµÄ“śŹżŹ½·Ö±š±ķŹ¾£ŗ
Ö±½ÓÓĆŗ¬tµÄ“śŹżŹ½·Ö±š±ķŹ¾£ŗ![]() ______£¬
______£¬![]() ______£»
______£»
![]() ŹĒ·ń“ęŌŚtµÄÖµ£¬Ź¹ĖıߊĪPDBQĪŖĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ēó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
ŹĒ·ń“ęŌŚtµÄÖµ£¬Ź¹ĖıߊĪPDBQĪŖĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ēó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
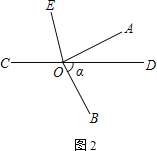
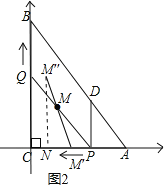
![]() ČēĶ¼2£¬ŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬Ēó³öĻ߶ĪPQÖŠµćMĖł¾¹żµÄĀ·¾¶³¤£®
ČēĶ¼2£¬ŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬Ēó³öĻ߶ĪPQÖŠµćMĖł¾¹żµÄĀ·¾¶³¤£®
”¾“š°ø”æ£Ø1£©![]() £¬
£¬![]() £»£Ø2£©Ļź¼ū½āĪö£»£Ø3£©2
£»£Ø2£©Ļź¼ū½āĪö£»£Ø3£©2![]()
”¾½āĪö”æ
![]() ÓÉøł¾ŻĀ·³ĢµČÓŚĖŁ¶Č³ĖŅŌŹ±¼äæɵĆ,
ÓÉøł¾ŻĀ·³ĢµČÓŚĖŁ¶Č³ĖŅŌŹ±¼äæɵĆ,![]() ,
,![]() ,Ōņ
,Ōņ![]() ,øł¾Ż
,øł¾Ż![]() ,
,![]() ,æɵĆ:
,æɵĆ:![]() ,øł¾ŻĻąĖĘČż½ĒŠĪµÄÅŠ¶ØæɵĆ:
,øł¾ŻĻąĖĘČż½ĒŠĪµÄÅŠ¶ØæɵĆ:![]() ”×
”×![]() ,ŌŁøł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹæɵĆ:
,ŌŁøł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹæɵĆ:
![]() ,¼“
,¼“![]() ,“Ó¶ų½āµĆ:
,“Ó¶ų½āµĆ:![]() ,
,
(2)øł¾Ż![]() ,µ±
,µ±![]() Ź±,æÉÅŠ¶ØĖıߊĪPDBQĪŖĘ½ŠŠĖıߊĪ,øł¾ŻĘ½ŠŠĖıߊĪµÄŠŌÖŹæɵĆ:
Ź±,æÉÅŠ¶ØĖıߊĪPDBQĪŖĘ½ŠŠĖıߊĪ,øł¾ŻĘ½ŠŠĖıߊĪµÄŠŌÖŹæɵĆ:![]() ,½āµĆ:
,½āµĆ:![]() ,
,
(3)øł¾ŻĢāŅāæɵĆ:![]() ,µ±
,µ±![]() Ź±,µć
Ź±,µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() ,µ±
,µ±![]() Ź±,µć
Ź±,µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() ,
,
ÉčÖ±Ļß![]() µÄ½āĪöŹ½ĪŖ:
µÄ½āĪöŹ½ĪŖ:![]() ,Ōņ
,Ōņ![]() ,½āµĆ:
,½āµĆ:![]() ,Ņņ“ĖÖ±Ļß
,Ņņ“ĖÖ±Ļß![]() µÄ½āĪöŹ½ĪŖ:
µÄ½āĪöŹ½ĪŖ:![]() ,ŌŁøł¾ŻĢāŅāµĆ:µćPµÄ×ų±źĪŖ
,ŌŁøł¾ŻĢāŅāµĆ:µćPµÄ×ų±źĪŖ![]() ,µćQµÄ×ų±źĪŖ
,µćQµÄ×ų±źĪŖ![]() ,Ņņ“ĖŌŚŌĖ¶Æ¹ż³ĢÖŠPQµÄÖŠµćMµÄ×ų±źĪŖ
,Ņņ“ĖŌŚŌĖ¶Æ¹ż³ĢÖŠPQµÄÖŠµćMµÄ×ų±źĪŖ![]() ,µ±
,µ±![]() Ź±,
Ź±,![]() ,Ņņ“ĖµćMŌŚÖ±Ļß
,Ņņ“ĖµćMŌŚÖ±Ļß![]() ÉĻ,×÷
ÉĻ,×÷![]() ÖįÓŚN,Ōņ
ÖįÓŚN,Ōņ![]() ,
,![]() ,Óɹ“¹É¶ØĄķµĆ,
,Óɹ“¹É¶ØĄķµĆ,![]() ,
,
Ņņ“ĖĻ߶ĪPQÖŠµćMĖł¾¹żµÄĀ·¾¶³¤ĪŖ![]() .
.
![]() ÓÉĢāŅāµĆ,
ÓÉĢāŅāµĆ,![]() ,
,![]() ,
,
Ōņ![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ”×
”×![]() ,
,
![]() ,¼“
,¼“![]() ,
,
½āµĆ:![]() ,
,
¹Ź“š°øĪŖ:![]() ,
,![]() ,
,
![]() “ęŌŚ,
“ęŌŚ,
![]() ,
,
![]() µ±
µ±![]() Ź±,ĖıߊĪPDBQĪŖĘ½ŠŠĖıߊĪ,
Ź±,ĖıߊĪPDBQĪŖĘ½ŠŠĖıߊĪ,
![]() ,
,
½āµĆ:![]() ,
,
Ōņµ±![]() Ź±,ĖıߊĪPDBQĪŖĘ½ŠŠĖıߊĪ,
Ź±,ĖıߊĪPDBQĪŖĘ½ŠŠĖıߊĪ,
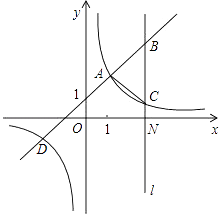
![]() ŅŌµćCĪŖŌµć,ŅŌACĖłŌŚµÄÖ±ĻßĪŖxÖį,½ØĮ¢ČēĶ¼2ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµ,
ŅŌµćCĪŖŌµć,ŅŌACĖłŌŚµÄÖ±ĻßĪŖxÖį,½ØĮ¢ČēĶ¼2ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµ,
ÓÉĢāŅāµĆ:![]() ,
,
µ±![]() Ź±,µć
Ź±,µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() ,
,
µ±![]() Ź±,µć
Ź±,µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() ,
,
ÉčÖ±Ļß![]() µÄ½āĪöŹ½ĪŖ:
µÄ½āĪöŹ½ĪŖ:![]() ,
,
Ōņ![]() ,
,
½āµĆ:![]() ,
,
![]() Ö±Ļß
Ö±Ļß![]() µÄ½āĪöŹ½ĪŖ£ŗ
µÄ½āĪöŹ½ĪŖ£ŗ![]() ,
,
ÓÉĢāŅāµĆ:µćPµÄ×ų±źĪŖ![]() ,µćQµÄ×ų±źĪŖ
,µćQµÄ×ų±źĪŖ![]() ,
,
![]() ŌŚŌĖ¶Æ¹ż³ĢÖŠPQµÄÖŠµćMµÄ×ų±źĪŖ
ŌŚŌĖ¶Æ¹ż³ĢÖŠPQµÄÖŠµćMµÄ×ų±źĪŖ![]() ,
,
µ±![]() Ź±,
Ź±,![]() ,
,
![]() µćMŌŚÖ±Ļß
µćMŌŚÖ±Ļß![]() ÉĻ,
ÉĻ,
×÷![]() ÖįÓŚN,
ÖįÓŚN,
Ōņ![]() ,
,![]() ,
,
Óɹ“¹É¶ØĄķµĆ,![]() ,
,
![]() Ļ߶ĪPQÖŠµćMĖł¾¹żµÄĀ·¾¶³¤ĪŖ
Ļ߶ĪPQÖŠµćMĖł¾¹żµÄĀ·¾¶³¤ĪŖ![]() .
.

 ĒįĖÉæĪĢƵ„ŌŖĘŚÖŠĘŚÄ©×ØĢā³å“Ģ100·ÖĻµĮŠ“š°ø
ĒįĖÉæĪĢƵ„ŌŖĘŚÖŠĘŚÄ©×ØĢā³å“Ģ100·ÖĻµĮŠ“š°ø