题目内容
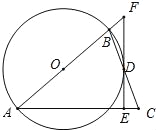
【题目】如图所示，直线AB, CD相交于点O，OF平分∠AOC，EO⊥CD于点O, 且∠DOF=160°，求∠BOE的度数；
【答案】130°
【解析】试题分析：由已知∠DOF=160°，先求其邻补角∠COF，再利用OF平分∠AOC，求∠AOC，然后利用互余关系求∠AOE，最后利用邻补角关系求∠BOE.
试题解析：
因为∠DOF+∠COF=180°，∠DOF =160°
所以∠COF=180°—∠DOF=180°—160°= 20°（2分）
又因为OF平分∠AOC,所以∠AOC=2∠COF=40°（1分）
所以∠DOB=∠AOC=40°（2分）
因为EO⊥CD,所以∠DOE=90°（1分）
所以∠BOE=∠DOE+∠DOB=90°+40°=130°.
练习册系列答案
优加精卷系列答案
相关题目
【题目】为庆祝“六一”儿童节，某市中小学统一组织文艺汇演，甲、乙两所学校共92人(其中甲校人数多于乙校人数，且甲校人数不够90人)准备统一购买服装参加演出，下面是某服装厂给出的演出服装的价格表：
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两校分别单独购买服装，一共应付5000元．
(1)如果甲、乙两校联合起来购买服装，那么比各自购买服装共可以节省多少钱？
(2)甲、乙两校各有多少学生准备参加演出？
(3)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出，请为两校设计一种省钱的购买服装方案．
