��Ŀ����
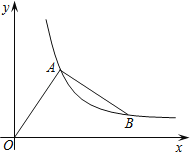
����Ŀ�������������400ǧ�ף�һ��������һ���γ��Ⱥ�Ӽس���ʻ���ҵأ���ͼ���߶�OA��ʾ������ص�·��y��ǧ�ף�������ʱ��x��Сʱ��֮��ĺ�����ϵ������BCD��ʾ�γ���ص�·��y��ǧ�ף���x��Сʱ��֮��ĺ�����ϵ������ͼ�����������⣺
��1�����߶�CD��Ӧ�ĺ�������ʽ��
��2����E������꣬������E���ʵ�����壻
��3������֪�γ��Ȼ���������20���ӣ��ҵ����ҵغ���ԭ�صȴ����������������������ͽγ����30ǧ��ʱ�����������ʱ�䣮

���㣺һ�κ�����Ӧ�ã�
���𰸡�
��������
�������:��1�����߶�CD��Ӧ�ĺ�������ʽΪy=kx+b���ɴ���ϵ���������⼴�ɣ�
��2��������ͼ���ཻ�Ľ���ָ��������������ɣ�
��3�����ɻ����ͽγ����30ǧ���г����̽�ɣ�
�⣺��1�����߶�CD��Ӧ�ĺ�������ʽΪy=kx+b��
�ɵã�![]() ��
��
��ã�![]() ��
��
�����߶�CD��Ӧ�ĺ�������ʽΪ��y=120x��140��2��x��4.5����
��2����ͼ��ɵã�ֱ��OA�Ľ���ʽΪ��y=80x��
������ͼ���ཻ�Ľ���ָ��������������
�ɵã�80x=120x��140��
��ã�x=3.5��
��x=3.5����y=80x���ã�y=280��
����E�������Ϊ��3.5��280��������ʾ����������3.5Сʱʱ�����ͽγ�������
��3�����������xh��
�ɵã�120x��140��30=80x��
��ã�x=4.25��
�ʴ�Ϊ��4.25��
��3��������֪��B��![]() ��0����
��0����
��BC�ν���ʽΪy=60x��20��![]() ��x��2����
��x��2����
���������30km�����������
1����![]() ��x��2ʱ��80x����60x��20��=30�����x=
��x��2ʱ��80x����60x��20��=30�����x=![]() ��
��
2����2��x��3.5ʱ��80x����120x��140��=30�����x=![]() ��
��
3����3.5��x��4.5ʱ��120x��140��80x=30�����x=![]() ��
��
4����4.5��x��5ʱ��400��80x=30�����x=![]() ��
��
��x=![]() ��
��