题目内容
【题目】综合与探究:
如图,抛物线y=![]() x2﹣
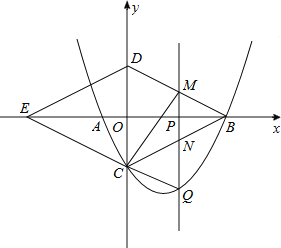
x2﹣![]() x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
考点:二次函数综合题.
【答案】
【解析】
试题分析:(1)根据坐标轴上点的特点,可求点A,B,C的坐标.
(2)由菱形的对称性可知,点D的坐标,根据待定系数法可求直线BD的解析式,根据平行四边形的性质可得关于m的方程,求得m的值;再根据平行四边形的判定可得四边形CQBM的形状;
(3)分DQ⊥BD,BQ⊥BD两种情况讨论可求点Q的坐标.
解:(1)当y=0时,![]() x2﹣
x2﹣![]() x﹣4=0,解得x1=﹣2,x2=8,
x﹣4=0,解得x1=﹣2,x2=8,
∵点B在点A的右侧,
∴点A的坐标为(﹣2,0),点B的坐标为(8,0).
当x=0时,y=﹣4,
∴点C的坐标为(0,﹣4).
(2)由菱形的对称性可知,点D的坐标为(0,4).
设直线BD的解析式为y=kx+b,则
![]() ,
,
解得k=﹣![]() ,b=4.
,b=4.
∴直线BD的解析式为y=﹣![]() x+4.
x+4.
∵l⊥x轴,
∴点M的坐标为(m,﹣![]() m+4),点Q的坐标为(m,
m+4),点Q的坐标为(m,![]() m2﹣
m2﹣![]() m﹣4).
m﹣4).
如图,当MQ=DC时,四边形CQMD是平行四边形,
∴(﹣![]() m+4)﹣(
m+4)﹣(![]() m2﹣
m2﹣![]() m﹣4)=4﹣(﹣4).
m﹣4)=4﹣(﹣4).
化简得:m2﹣4m=0,
解得m1=0(不合题意舍去),m2=4.
∴当m=4时,四边形CQMD是平行四边形.
此时,四边形CQBM是平行四边形.
解法一:∵m=4,
∴点P是OB的中点.
∵l⊥x轴,
∴l∥y轴,
∴△BPM∽△BOD,
∴![]() =
=![]() =
=![]() ,
,
∴BM=DM,
∵四边形CQMD是平行四边形,
∴DM![]() CQ,
CQ,
∴BM![]() CQ,
CQ,
∴四边形CQBM是平行四边形.
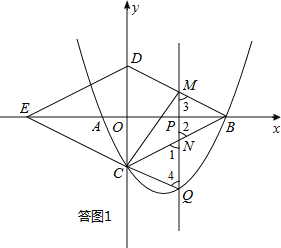
解法二:设直线BC的解析式为y=k1x+b1,则
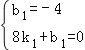 ,
,
解得k1=![]() ,b1=﹣4.
,b1=﹣4.
故直线BC的解析式为y=![]() x﹣4.
x﹣4.
又∵l⊥x轴交BC于点N,
∴x=4时,y=﹣2,
∴点N的坐标为(4,﹣2),
由上面可知,点M的坐标为(4,2),点Q的坐标为(4,﹣6).
∴MN=2﹣(﹣2)=4,NQ=﹣2﹣(﹣6)=4,
∴MN=QN,
又∵四边形CQMD是平行四边形,
∴DB∥CQ,
∴∠3=∠4,
∵在△BMN与△CQN中,
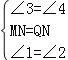 ,
,
∴△BMN≌△CQN(ASA)
∴BN=CN,
∴四边形CQBM是平行四边形.
(3)抛物线上存在两个这样的点Q,分别是Q1(﹣2,0),Q2(6,﹣4).
若△BDQ为直角三角形,可能有三种情形,如答图2所示:
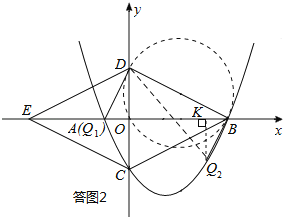
①以点Q为直角顶点.
此时以BD为直径作圆,圆与抛物线的交点,即为所求之Q点.
∵P在线段EB上运动,
∴﹣8≤xQ≤8,而由图形可见,在此范围内,圆与抛物线并无交点,
故此种情形不存在.
②以点D为直角顶点.
连接AD,∵OA=2,OD=4,OB=8,AB=10,
由勾股定理得:AD=![]() ,BD=
,BD=![]() ,
,
∵AD2+BD2=AB2,
∴△ABD为直角三角形,即点A为所求的点Q.
∴Q1(﹣2,0);
③以点B为直角顶点.
如图,设Q2点坐标为(x,y),过点Q2作Q2K⊥x轴于点K,则Q2K=﹣y,OK=x,BK=8﹣x.
易证△Q2KB∽△BOD,
∴![]() ,即
,即![]() ,整理得:y=2x﹣16.
,整理得:y=2x﹣16.
∵点Q在抛物线上,∴y=![]() x2﹣
x2﹣![]() x﹣4.
x﹣4.
∴![]() x2﹣
x2﹣![]() x﹣4=2x﹣16,解得x=6或x=8,
x﹣4=2x﹣16,解得x=6或x=8,
当x=8时,点Q2与点B重合,故舍去;
当x=6时,y=﹣4,
∴Q2(6,﹣4).
综上所述,符合题意的点Q的坐标为(﹣2,0)或(6,﹣4).

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案