题目内容
【题目】如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则![]() 的值等于 .
的值等于 .
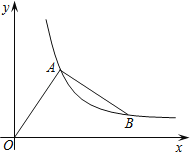
考点:反比例函数图象上点的坐标特征;坐标与图形变化-旋转.
【答案】
【解析】
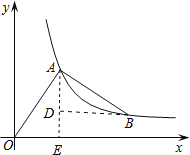
试题分析:过A作AE⊥x轴,过B作BD⊥AE,利用同角的余角相等得到一对角相等,再由一对直角相等,且AO=AB,利用AAS得出三角形AOE与三角形ABD全等,由确定三角形的对应边相等得到BD=AE=b,AD=OE=a,进而表示出ED及OE+BD的长,即可表示出B坐标;由A与B都在反比例图象上,得到A与B横纵坐标乘积相等,列出关系式,变形后即可求出![]() 的值.
的值.
解:过A作AE⊥x轴,过B作BD⊥AE,
∵∠OAB=90°,
∴∠OAE+∠BAD=90°,
∵∠AOE+∠OAE=90°,
∴∠BAD=∠AOE,
在△AOE和△BAD中,
 ,
,
∴△AOE≌△BAD(AAS),
∴AE=BD=b,OE=AD=a,
∴DE=AE﹣AD=b﹣a,OE+BD=a+b,
则B(a+b,b﹣a);
∵A与B都在反比例图象上,得到ab=(a+b)(b﹣a),
整理得:b2﹣a2=ab,即(![]() )2﹣
)2﹣![]() ﹣1=0,
﹣1=0,
∵△=1+4=5,
∴![]() =
=![]() ,
,
∵点A(a,b)为第一象限内一点,
∴a>0,b>0,
则![]() =
=![]() .
.
故答案为![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

