题目内容
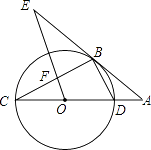
【题目】如图，点A在直线l上，点Q沿着直线l以3厘米/秒的速度由点A向右运动，以AQ为边作Rt△ABQ，使∠BAQ=90°，tan∠ABQ= 
，点C在点Q右侧，CQ=1厘米，过点C作直线m⊥l，过△ABQ的外接圆圆心O作OD⊥m于点D，交AB右侧的圆弧于点E．在射线CD上取点F，使DF= 
CD，以DE、DF为邻边作矩形DEGF．设运动时间为t秒．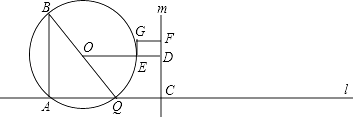
（1）直接用含t的代数式表示BQ、DF；
（2）当0＜t＜1时，求矩形DEGF的最大面积；
（3）点Q在整个运动过程中，当矩形DEGF为正方形时，求t的值．
【答案】
（1）解：∵点Q沿着直线l以3厘米/秒的速度由点A向右运动，运动时间为t秒．
∴AQ=3t，
∵∠BAQ=90°，tan∠ABQ= 
= 
，
∴AB=4t，
∴BQ= 
=5t，
作OM⊥AQ于M，则AM=QM= 
AQ=1.5t，CD=OM，
∴OM是△ABQ的中位线，
∴CD=OM= AB=2t，
∴DF= 
CD= 
t
（2）解：设矩形DEGF的面积为S，
∵OE=OB= BQ= 
t，OD=QM+CQ= 
t+1，
∴DE=OD﹣OE= t+1﹣ t=1﹣t，
∴ 
，
∴当t= 时，矩形DEGF的最大面积为 
（3）解：当矩形DEGF为正方形时，则DE=DF，分两种情况：
①当0＜t＜1时，如图1所示：
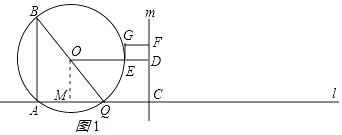
DE=1﹣t，
∴1﹣t= t，
解得：t= 
；
②当t≥1时，如图2所示：
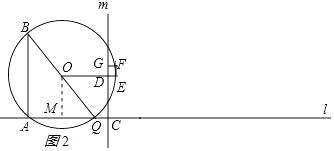
DE=t﹣1，
∴t﹣1= t，
解得：t=3；
综上所述：当矩形DEGF为正方形时，t的值为 或3．
【解析】（1）由已知得出AQ=3t，由三角函数求出AB=4t，再由勾股定理求出BQ= 5t，作OM⊥AQ于M，则AM=QM= AQ=1.5t，CD=OM，由三角形的中位线定理得出CD=OM= AB=2t，进而得出结论；
（2）设矩形DEGF的面积为S，OE= t，OD=QM+CQ= t+1，
∴DE=OD﹣OE= t+1﹣ t=1﹣t，由矩形的面积得出s是t的二次函数，即可得出答案；
（3）当矩形DEGF为正方形时，则DE=DF，分两种情况：①当0＜t＜1时，如图1所示得出方程，解方程即可；②当t≥1时，如图2所示：DE=t﹣1，得出方程，解方程即可。
【考点精析】解答此题的关键在于理解二次函数的最值的相关知识，掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
