题目内容
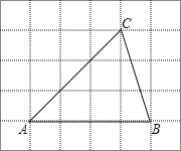
【题目】如图，将
放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．
Ⅰ
的面积等于______；
Ⅱ
若四边形DEFG是中所能包含的面积最大的正方形，请你在如图所示的网格中，用直尺和三角尺画出该正方形，并简要说明画图方法不要求证明________________．
【答案】6 见解析
【解析】
（Ⅰ）△ABC以AB为底，高为3个单位，求出面积即可；
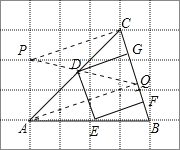
（Ⅱ）作出所求的正方形，如图所示，画图方法为：取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，则四边形DEFG即为所求
解：（Ⅰ）△ABC的面积为：
；
（Ⅱ）如图，取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，
则四边形DEFG即为所求．
证明：根据题意得当正方形DEFG各个顶点都在△ABC的边上时，其面积才有可能最大，则必有两点在三角形一边上，此时四边形内接于三角形，
根据三角形内接正方形的性质，锐角三角形的最大内接正方形是以三角形的最短边为底形成的正方形，
如图所示作出符合要求的四边形DEFG，
可知：DG∥AQ∥EF∥PC，DE∥GF，
∴四边形DEFG是平行四边形，
且△DGQ∽△PCQ，△ADE∽△ACB，△CDP∽△ADQ，
∴
，
，
，
则DG=
，DE=
，
∵PC⊥BC，
∴DG⊥GF，
则四边形DEFG是矩形，
∵PC=BC，，
∴DG=
=
，
=
=
=
=
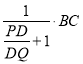
=DE，
∴矩形DEFG是正方形.
故答案为：（Ⅰ）6；（Ⅱ）取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，则四边形DEFG即为所求．
