��Ŀ����
����Ŀ����ͼ����֪һ�κ���y=��x+7������������y= ![]() x��ͼ���ڵ�A������x�ύ�ڵ�B��
x��ͼ���ڵ�A������x�ύ�ڵ�B��
��1�����A�͵�B�����ꣻ
��2������A��AC��y���ڵ�C������B��ֱ��l��y�ᣮ����P�ӵ�O��������ÿ��1����λ�����ٶȣ���O��C��A��·�����A�˶���ͬʱֱ��l�ӵ�B����������ͬ�ٶ�����ƽ�ƣ���ƽ�ƹ����У�ֱ��l��x���ڵ�R�����߶�BA���߶�AO�ڵ�Q������P�����Aʱ����P��ֱ��l��ֹͣ�˶������˶������У��趯��P�˶���ʱ��Ϊt�룮
�ٵ�tΪ��ֵʱ����A��P��RΪ����������ε����Ϊ8��
���Ƿ������A��P��QΪ������������ǵ��������Σ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��һ�κ���y=��x+7������������y= ![]() x��ͼ���ڵ�A������x�ύ�ڵ�B��
x��ͼ���ڵ�A������x�ύ�ڵ�B��
�� 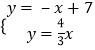 ��
��
��ã� ![]() ��
��
��A����������3��4����
��y=��x+7=0��
��ã�x=7��
��B����������7��0��
��2��
�⣺�ٵ�P��OC���˶�ʱ��0��t��4ʱ��PO=t��PC=4��t��BR=t��OR=7��t��
�ߵ���A��P��RΪ����������ε����Ϊ8��
��S����ACOB��S��ACP��S��POR��S��ARB=8��
�� ![]() ��AC+BO����CO��
��AC+BO����CO�� ![]() AC��CP��
AC��CP�� ![]() PO��RO��
PO��RO�� ![]() AM��BR=8��
AM��BR=8��
�ࣨAC+BO����CO��AC��CP��PO��RO��AM��BR=16��
�ࣨ3+7����4��3����4��t����t����7��t����4t=16��
��t2��8t+12=0��
��ã�t1=2��t2=6����ȥ����
��t=4ʱ�������������Σ�
��4��t��7ʱ��S��APR= ![]() AP��OC=2��7��t��=8�����t=3��������4��t��7��
AP��OC=2��7��t��=8�����t=3��������4��t��7��
������������t=2ʱ����A��P��RΪ����������ε����Ϊ8��
�ڴ��ڣ��ӳ�CA��ֱ��l����һ��D����l��AB�ཻ��Q��
��һ�κ���y=��x+7��x�ύ�ڣ�7��0���㣬��y�ύ�ڣ�0��7���㣬
��NO=OB��
���OBN=��ONB=45�㣬
��ֱ��l��y�ᣬ
��RQ=RB��CD��L��
��0��t��4ʱ����ͼ1��
RB=OP=QR=t��DQ=AD=��4��t����AC=3��PC=4��t��
����A��P��QΪ������������ǵ��������Σ���AP=AQ��
��AC2+PC2=AP2=AQ2=2AD2��
��9+��4��t��2=2��4��t��2����ã�t1=1��t2=7����ȥ����
��AP=PQʱ 32+��4��t��2=��7��t��2��
���t=4 ����ȥ��
��PQ=AQʱ��2��4��t��2=��7��t��2��
���t1=1+3 ![]() ����ȥ����t2=1��3
����ȥ����t2=1��3 ![]() ����ȥ����
����ȥ����
��t=4ʱ�������������Σ�
��4��t��7ʱ����ͼ������ͼ������A��AD��OB��D����AD=BD=4��
��ֱ��l��AC��E����QE��AC��AE=RD=t��4��AP=7��t��
��cos��OAC= ![]() =
= ![]() ��
��
��AQ= ![]() ��t��4����
��t��4����
��AQ=AP���� ![]() ��t��4��=7��t�����t=
��t��4��=7��t�����t= ![]() ��
��
��AQ=PQʱ��AE=PE����AE= ![]() AP��
AP��
��t��4= ![]() ��7��t����
��7��t����
��ã�t=5��
��AP=PQʱ����P��PF��AQ��F��
AF= ![]() AQ=
AQ= ![]() ��
�� ![]() ��t��4����
��t��4����
��Rt��APF����cos��PAF= ![]() =
= ![]() ��
��
��AF= ![]() AP��
AP��
�� ![]() ��
�� ![]() ��t��4��=
��t��4��= ![]() ��7��t����
��7��t����
��ã�t= ![]() ��
��
������������t=1��5�� ![]() ��
�� ![]() ʱ��������A��P��QΪ������������ǵ��������Σ�
ʱ��������A��P��QΪ������������ǵ��������Σ�

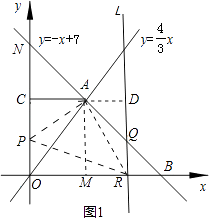
����������1������ͼ���������ύ����ֱ�ӵó����ɣ�������ֱ�߽�����������ֱ�߽���ʽ�������ɵó��������ꣻ��2��������S����ACOB��S��ACP��S��POR��S��ARB=8����ʾ�������ֵı߳���������һԪ���η��̣�������ɣ��ڸ���һ�κ�����������Ľ���ó�����OBN=��ONB=45�㣬�������ù��ɶ����Լ����������ε����ʺ�ֱ�������ε��ж�������ɣ�
�����㾫��������һ�κ�����ͼ������ʺ͵��������ε������ǽ����ĸ�������Ҫ֪��һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ�����������ε���������ȣ���ƣ��ȱ߶ԵȽǣ���

 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�







