Question

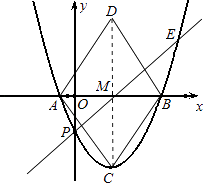
【题目】如图，已知二次函数y=x2+bx+c的图象与x轴交于A，B两点，与y轴交于点P，顶点为C（1，﹣2）．

（1）求此函数的关系式；
（2）作点C关于x轴的对称点D，顺次连接A，C，B，D．若在抛物线上存在点E，使直线PE将四边形ACBD分成面积相等的两个四边形，求点E的坐标；
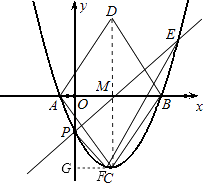
（3）在（2）的条件下，抛物线上是否存在一点F，使得△PEF是以P为直角顶点的直角三角形？若存在，求出点F的坐标及△PEF的面积；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵y=x2+bx+c的顶点为（1，﹣2）．

∴y=（x﹣1）2﹣2=x2﹣2x﹣1

（2）

解：设直线PE对应的函数关系式为y=kx+b，根据A，B关于对称轴对称，

可以得出AC=CB，AD=BD，点C关于x轴的对称点D，

故AC=BC=AD=BD，

则四边形ACBD是菱形，

故直线PE必过菱形ACBD的对称中心M．

由P（0，﹣1），M（1，0），

得

从而得y=x﹣1，

设E（x，x﹣1）代入y=x2﹣2x﹣1得x﹣1=x2﹣2x﹣1，

解得x1=0，x2=3，

根据题意得点E（3，2）

（3）

解：假设存在这样的点F，可设F（x，x2﹣2x﹣1），

过点F做FG⊥y轴，垂足为G点．

在Rt△POM和Rt△FGP中，

∵∠OMP+∠OPM=90°，∠FPG+∠OPM=90°，

∠OMP=∠FPG，

又∠MOP=∠PGF，

∴△POM∽△FGP

∴

∵OM=1，OP=1，

∴GP=GF，即﹣1﹣（x2﹣2x﹣1）=x，

解得x1=0，x2=1，

根据题意得F（1，﹣2）

以上各步均可逆，故点F（1，﹣2）即为所求，

S△PEF=S△MFP+S△MFE= 2×1 ×2×2=3．

【解析】（1）将顶点坐标C（1，﹣2）代入y=x2+bx+c即可求得此二次函数的关系式；（2）先求出直线PM的解析式，然后与二次函数联立即可解得点E的坐标；（3）根据三角形相似的性质先求出GP=GF，求出F点的坐标，进而求得△PEF的面积．