Question

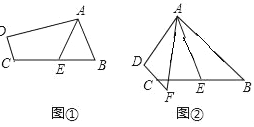
【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB＝AC，直线l经过点A，BD⊥直线l，CE⊥直线l，垂足分别为点D、E．证明：DE＝BD+CE．

（2）如图（2），将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线l上，且∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立；请你给出证明；若不成立，请说明理由．

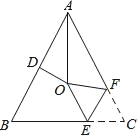
（3）拓展与应用：如图（3），D、E是直线l上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，求证：DF＝EF．

Answer 1

【答案】(1)见解析;(2)见解析;(3)见解析.

【解析】

（1）由条件可证明△ABD≌△CAE，可得DA＝CE，AE＝BD，可得DE＝BD+CE；

（2）由条件可知∠BAD+∠CAE＝180°﹣α，且∠DBA+∠BAD＝180°﹣α，可得∠DBA＝∠CAE，结合条件可证明△ABD≌△CAE，同（1）可得出结论．

（3）由（2）知，△ADB≌△CAE，得到BD＝EA，∠DBA＝∠CAE，再△DBF≌△EAF（SAS），得到DF＝EF，∠BFD＝∠AFE，求出∠DFE＝∠DFA+∠AFE＝∠DFA+∠BFD＝60°，所以△DEF为等边三角形．即可得到DF＝EF．

解：（1）∵BD⊥l，CE⊥l，

∴∠BDA＝∠AEC＝90°

又∵∠BAC＝90°，

∴∠BAD+∠CAE＝90°，∠BAD+∠ABD＝90°，

∴∠CAE＝∠ABD

在△ABD和△CAE中，

，

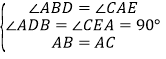∴△ABD≌△CAE（AAS）

∴BD＝AE，AD＝CE，

∵DE＝AD+AE，

∴DE＝CE+BD；

（2）成立

∵∠BDA＝∠AEC＝∠BAC＝α，

∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，

∴∠CAE＝∠ABD，

在△ADB和△CEA中，

，

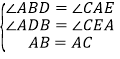∴△ADB≌△CEA（AAS），

∴AE＝BD，AD＝CE，

∴BD+CE＝AE+AD＝DE；

（3）由（2）知，△ADB≌△CAE，

∴BD＝EA，∠DBA＝∠CAE，

∵△ABF和△ACF均为等边三角形，

∴∠ABF＝∠CAF＝60°，

∴∠DBA+∠ABF＝∠CAE+∠CAF，

∴∠DBF＝∠FAE，

∵BF＝AF

在△DBF和△EAF中，

，

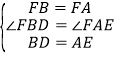∴△DBF≌△EAF（SAS），

∴DF＝EF，∠BFD＝∠AFE，

∴∠DFE＝∠DFA+∠AFE＝∠DFA+∠BFD＝60°，

∴△DEF为等边三角形．

∴DF＝EF．