题目内容
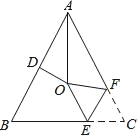
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)小明同学用3张边长为a的正方形,4张边长为b的正方形,7张边长分别为a、b的长方形纸片拼出了一个长方形,那么该长方形较长一边的边长为多少?
(4)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出了一个面积为(5a+7b)(4a+9b)长方形,那么x+y+z= .
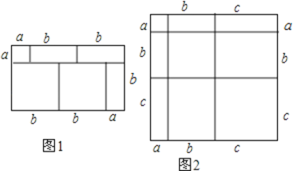
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)45;(3)3a+4b ;(4)156
【解析】
(1)直接求得正方形的面积,然后再根据正方形的面积=各矩形的面积之和求解即可;
(2)将a+b+c=11,ab+bc+ac=38代入(1)中得到的关系式,然后进行计算即可;
(3)先列出长方形的面积的代数式,然后分解代数式,可得到矩形的两边长;
(4)长方形的面积xa2+yb2+zab=(5a+7b)(4a+9b),然后运算多项式乘多项式法则求得(5a+7b)(4a+9b)的结果,从而得到x、y、z的值.
解:(1)正方形的面积可表示为=(a+b+c)2;
正方形的面积=各个矩形的面积之和=a2+b2+c2+2ab+2bc+2ca,
所以(a+b+c)2=a2+b2+c2+2ab+2bc+2ca.
(2)a2+b2+c2=(a+b+c)2-2ab-2ac-2bc,
=112-2×38,
=45;
(3)长方形的面积=3a2+7ab+4b2=(3a+4b)(a+b).
所以长方形的边长为3a+4b和a+b,
所以较长的一边长为3a+4b;
(4)∵长方形的面积=xa2+yb2+zab=(5a+7b)(4a+9b)
= 20a2+63b2+73ab,
∴x=20,y=63,z=73.
∴x+y+z=20+63+73=156.
故答案为:156.

 阅读快车系列答案
阅读快车系列答案【题目】如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层、第二层…第n层,第n层的小正方体的个数记为S.解答下列问题:
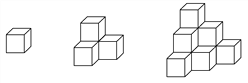
n | 1 | 2 | 3 | 4 | … |
S | 1 | 3 | … |
(1)按要求填写上表:
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?