МвДїДЪИЭ
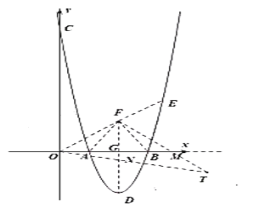
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ЕЧОпПЯ![]() Ѕ»
Ѕ»![]() ЦбУЪ
ЦбУЪ![]() Ј¬
Ј¬![]() БЅµгЈЁµг
БЅµгЈЁµг![]() ФЪµг
ФЪµг![]() µДЧу±ЯЈ©Ѕ»
µДЧу±ЯЈ©Ѕ»![]() ЦбХэ°лЦбУЪµг
ЦбХэ°лЦбУЪµг![]() Ј¬µг
Ј¬µг![]() ОЄЕЧОпПЯ¶Ґµг.
ОЄЕЧОпПЯ¶Ґµг.
ЈЁ1Ј©Ц±ЅУРґіц![]() ИэµгµДЧш±кј°
ИэµгµДЧш±кј°![]() µДЦµЈ»
µДЦµЈ»
ЈЁ2Ј©µг![]() ОЄЕЧОпПЯФЪ
ОЄЕЧОпПЯФЪ![]() ЦбЙП·ЅµДТ»µгЈ¬ЗТ
ЦбЙП·ЅµДТ»µгЈ¬ЗТ![]() Ј¬Зуµг
Ј¬Зуµг![]() µДЧш±кЈ»
µДЧш±кЈ»
ЈЁ3Ј©ФЪЈЁ2Ј©µДМхјюПВЈ¬![]() ОЄ
ОЄ![]() µДНвРДЈ¬µг
µДНвРДЈ¬µг![]() Ј¬µг
Ј¬µг![]() ·Ц±рґУµг
·Ц±рґУµг![]() Н¬К±іц·ўТФ2µҐО»/
Н¬К±іц·ўТФ2µҐО»/![]() Ј¬1µҐО»/
Ј¬1µҐО»/![]() ЛЩ¶ИСШЙдПЯ
ЛЩ¶ИСШЙдПЯ![]() Ј¬
Ј¬![]() ЧчФИЛЩФЛ¶ЇЈ¬ФЛ¶ЇК±јдОЄ
ЧчФИЛЩФЛ¶ЇЈ¬ФЛ¶ЇК±јдОЄ![]() ГлЈЁ
ГлЈЁ![]() ЗТ
ЗТ![]() Ј©Ј¬Ц±ПЯ
Ј©Ј¬Ц±ПЯ![]() Ѕ»УЪ
Ѕ»УЪ![]() .
.
ўЩЗуЦ¤Јєµг![]() ФЪ¶ЁЦ±ПЯ
ФЪ¶ЁЦ±ПЯ![]() ЙПІўЗу
ЙПІўЗу![]() µДЅвОцКЅЈ»
µДЅвОцКЅЈ»
ўЪИф![]() ФЪЕЧОпПЯЙПЗТФЪЦ±ПЯ
ФЪЕЧОпПЯЙПЗТФЪЦ±ПЯ![]() ПВ·ЅЈ¬µ±
ПВ·ЅЈ¬µ±![]() µЅЦ±ПЯ
µЅЦ±ПЯ![]() ѕаАлЧоґуК±Ј¬Зуµг
ѕаАлЧоґуК±Ј¬Зуµг![]() µДЧш±к.
µДЧш±к.
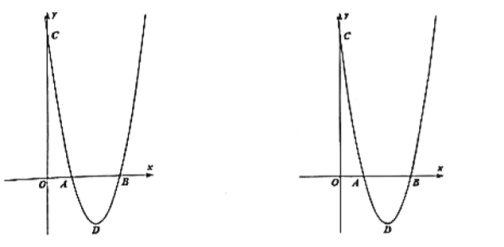
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]() Ј»ЈЁ3Ј©ўЩ
Ј»ЈЁ3Ј©ўЩ![]() Ј¬јыЅвОцЈ¬ўЪ
Ј¬јыЅвОцЈ¬ўЪ![]()
ЎѕЅвОцЎї
ЈЁ1Ј©Ѕ«y=0Ј¬x=0ґъИлјґїЙРґіц![]() ИэµгµДЧш±кј°
ИэµгµДЧш±кј°![]() µДЦµЈ»
µДЦµЈ»
ЈЁ2Ј©ПИЗу![]() µДЅвОцКЅОЄ
µДЅвОцКЅОЄ![]() Ј¬БЄБў
Ј¬БЄБў![]() ЅвµГЈє
ЅвµГЈє![]() ЈЁЙбИҐЈ©Ј¬
ЈЁЙбИҐЈ©Ј¬![]() Ј¬їЙµГ
Ј¬їЙµГ![]() .
.
ЈЁ3Ј©ўЩЙи![]() Ј¬Фт
Ј¬Фт![]() Ј¬їЙ
Ј¬їЙ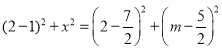 ЅвµГЈє
ЅвµГЈє![]() Ј¬
Ј¬![]() Ј¬Йи
Ј¬Йи![]() Ј¬Фт
Ј¬Фт![]() Ј¬µ±
Ј¬µ±![]() К±Ј¬
К±Ј¬![]() їЙµГ
їЙµГ![]() µ±
µ±![]() К±Ј¬Н¬АнїЙЗу
К±Ј¬Н¬АнїЙЗу![]() Ј¬№К
Ј¬№К![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ЙП.
ЙП.
ўЪµ±![]() µЅ
µЅ![]() ѕаАлЧоґуК±Ј¬Йи№э
ѕаАлЧоґуК±Ј¬Йи№э![]() ЗТУл
ЗТУл![]() ЖЅРРµДЦ±ПЯµДЅвОцКЅОЄЈє
ЖЅРРµДЦ±ПЯµДЅвОцКЅОЄЈє ![]() БЄБў
БЄБў![]() АыУГёГ·ЅіМЧйУРБЅёцПаµИµДКµКэёщЈ¬їЙµГ·ЅіМ
АыУГёГ·ЅіМЧйУРБЅёцПаµИµДКµКэёщЈ¬їЙµГ·ЅіМ![]() УРБЅёцПаµИµДКµКэёщЈ¬ЗуµГ
УРБЅёцПаµИµДКµКэёщЈ¬ЗуµГ![]() Ј¬№К
Ј¬№К![]() Ј¬їЙµГµг
Ј¬їЙµГµг![]() µДЧш±к.
µДЧш±к.
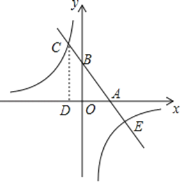
ЈЁ1Ј©ЎЯЕЧОпПЯ![]() Ј¬µг
Ј¬µг![]() ОЄЕЧОпПЯ¶Ґµг.
ОЄЕЧОпПЯ¶Ґµг.
Ўа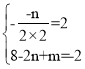
ЅвµГ![]()
Ўа![]()
µ±y=0К±Ј¬![]()
ЅвµГ![]()
Ўа![]()
µ±x=0К±Ј¬![]()
ЅвµГ![]()
Ўа![]()
Ўа![]()
ЈЁ2Ј©ЎЯ![]()
Ўа![]()
Йи![]() µДЅвОцКЅОЄ
µДЅвОцКЅОЄ![]()
УЦТтОЄAЈЁ1Ј¬0Ј©.ґъИл![]() ЅвµГЈєb=-1
ЅвµГЈєb=-1
№К![]() µДЅвОцКЅОЄ
µДЅвОцКЅОЄ![]() Ј¬
Ј¬
Ўа![]()
ЅвµГЈє![]() ЈЁЙбИҐЈ©Ј¬
ЈЁЙбИҐЈ©Ј¬![]() Ј¬
Ј¬
Ўа![]() .
.
ЈЁ3Ј©ўЩЙи![]() Ј¬
Ј¬![]() Ј¬
Ј¬
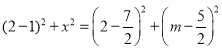
ЅвµГЈє![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Йи![]() Ј¬
Ј¬![]() Ј¬
Ј¬
µ±![]() К±Ј¬
К±Ј¬![]()
µ±![]() К±Ј¬Н¬АнїЙЗу
К±Ј¬Н¬АнїЙЗу![]() Ј¬№К
Ј¬№К![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ЙП.
ЙП.
ўЪµ±![]() µЅ
µЅ![]() ѕаАлЧоґуК±Ј¬Йи№э
ѕаАлЧоґуК±Ј¬Йи№э![]() ЗТУл
ЗТУл![]() ЖЅРРµДЦ±ПЯµДЅвОцКЅОЄЈє
ЖЅРРµДЦ±ПЯµДЅвОцКЅОЄЈє
![]()
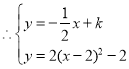 УРБЅµИёщ
УРБЅµИёщ
![]() УРµИёщЈ¬
УРµИёщЈ¬![]()
![]()