Question

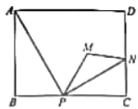
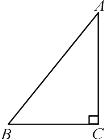
【题目】如图，在Rt△ABC中，∠C=90°，AC=8，sin A=

(1)求AB的长;

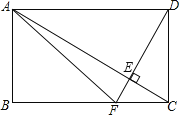
(2)若点E在Rt△ABC的直角边上，点F在斜边AB上，当△CFE∽△ABC时，求CE的长.

Answer 1

【答案】（1）AB=10（2）4或

【解析】

（1）由在Rt△ABC中，∠C=90°，sin A=，可设设BC=3x，AB=5x，求得AC=4x，进而求出AB的值；

（2）当△CFE∽△ABC时，分两种情况：①当点E在AB上，②当点E在BC上，分别求出CE的长，即可.

（1）∵在Rt△ABC中，∠C=90°，sin A=，

设BC=3x，AB=5x，则，

∵AC=8，

∴4x=8，解得：x=2，

∴AB=5x=5×2=10.

（2）分两种情况：

①当点E在AB上时，△CFE∽△ABC，如图1，

∴∠FEC=∠BCA=90°，∠ECF=∠CAB，

∴AE=CE（等腰三角形三线合一）

∵AC=8，

∴CE=4；

②当点E在BC上时，△CFE∽△ABC，如图2，

∴∠ECF=∠CAB，，

∵∠CAB+∠ACF=∠ECF+∠ACF=90°，

∴CF⊥AB，

∴CF==4.8，

∴=4.8×=

图1 图2