Question

【题目】如图，一张正方形纸板的边长为2cm，将它剪去4个全等的直角三角形（图中阴影部分）．设AE=BF=CG=DH=xcm，四边形EFGH的面积为ycm2 ，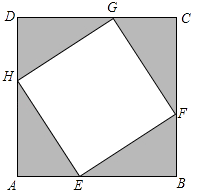

（1）求y关于x的函数表达式和自变量x的取值范围；
（2）求四边形EFGH的面积为3cm2时的x值；
（3）四边形EFGH的面积可以为1.5cm2吗？请说明理由．

Answer 1

【答案】
（1）解：∵在正方形纸上剪去4个全等的直角三角形，

∴∠AHE=∠DGH，∠DGH+∠DHG=90°，HG=HE，

∵∠EHG=180°﹣∠AHE﹣∠DHG，

∴∠EHG=90°，四边形EFGH为正方形，

在△AEH中，AE=x，AH=BE=AB﹣AE=2﹣x，∠A=90°，

∴HE2=AE2+AH2=x2+（2﹣x）2=2x2﹣4x+4，

正方形EFGH的面积y=HE2=2x2﹣4x+4，

∵AE，AH均为正值，

∴0＜x＜2，

故y关于x的函数表达式为：y=2x2﹣4x+4，自变量x的取值范围0＜x＜2．

（2）解：将y=3代入y=2x2﹣4x+4中，整理得：2x2﹣4x+1=0，

解得：x1=1+ ，x2=1﹣ ，

故四边形EFGH的面积为3cm2时的x的值为1+ 或1﹣ ．

（3）解：四边形EFGH的面积为：y=2x2﹣4x+4=2（x﹣1）2+2，（0＜x＜2），

∵（x﹣1）2≥0，

∴y≥2，

四边形EFGH的面积不能为1.5cm2．

【解析】（1）先证出四边形EFGH为正方形，用未知数x表示其任一边长，根据正方形面积公式即可解决问题；（2）代入y值，解一元二次方程即可；（3）将面积y=2x2﹣4x+4改写成完全平方的形式，可得知y≥2，故不能为cm2 ．