题目内容
【题目】在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣ax+6与x轴负半轴交于点A,与x轴的正半轴交于点B,且AB=7.
(1)如图1,求a的值;
(2)如图2,点P在第一象限内抛物线上,过P作PH∥AB,交y轴于点H,连接AP,交OH于点F,设HF=d,点P的横坐标为t,求d与t之间的函数关系式,并直接写出t的取值范围;
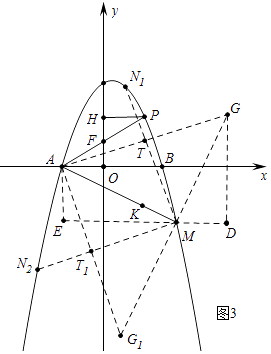
(3)如图3,在(2)的条件下,当PH=2d时,将射线AP沿着x轴翻折交抛物线于点M,在抛物线上是否存在点N,使∠AMN=45°,若存在,求出点N的坐标.若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=ax2﹣ax+6与x轴负半轴交于点A,与x轴的正半轴交于点B,且AB=7,
又∵对称轴x=﹣ ![]() =
= ![]() ,
,
∴A(﹣3,0),B(4,0),
把(﹣3,0)代入y=ax2﹣ax+6得a=﹣ ![]()
(2)
解:由抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+6,设P(t,﹣
x+6,设P(t,﹣ ![]() t2+
t2+ ![]() t+6),
t+6),
∵PH∥OA,HF=d,OF=﹣ ![]() t2+
t2+ ![]() t+6﹣d,PH=t,OA=3,
t+6﹣d,PH=t,OA=3,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴d= ![]() t=﹣
t=﹣ ![]() +2t(0<t<4)
+2t(0<t<4)
(3)
解:∵t=PH=2d,
∴d= ![]() ,
,
∴ ![]() =﹣
=﹣ ![]() t2+2t,
t2+2t,
解得t=3或0(舍弃),
∴P(3,3),点P关于x轴的对称点K(3,﹣3),
∴直线AM的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
由 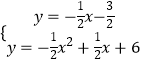 解得
解得 ![]() 或
或 ![]() ,
,
∵A(﹣3,0),
∴M(5,﹣4),
如图3中,将线段MA绕点M顺时针旋转90°得到线段MG,过点A作y轴的平行线,过点M作x轴的平行线,两直线交于点E,作GD⊥EM交EM的延长线于D.
易知△AME≌△MGD,∴AE=DM=4,EM=DG=8,
∴G(9,4),
取线段AG的中点T(3,2),作直线MT交抛物线于N1,此时∠AMN1=45°,
∵直线MT的解析式为y=﹣3x+11,
由 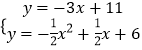 解得
解得 ![]() 或
或 ![]() ,
,
∵M(5,﹣4),
∴N1(2,5).
设点G关于直线AM的对称点为G1,则G1(1,﹣12),取AG1的中点T1,作直线MT1交抛物线于N2,则∠N2MA=45°,
∵直线MT1的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
由 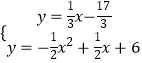 解得
解得 ![]() 或
或 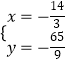 ,
,
∵M(5,﹣4),
∴N2(﹣ ![]() ,﹣
,﹣ ![]() ).
).
综上所述,满足条件的点M的坐标为(2,5)或(﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)根据对称轴x= ![]() ,以及AB=7,可得A(﹣3,0),B(4,0),利用待定系数法即可求出a的值.(2)由抛物线的解析式为y=﹣
,以及AB=7,可得A(﹣3,0),B(4,0),利用待定系数法即可求出a的值.(2)由抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+6,设P(t,﹣
x+6,设P(t,﹣ ![]() t2+
t2+ ![]() t+6),由PH∥OA,HF=d,OF=﹣
t+6),由PH∥OA,HF=d,OF=﹣ ![]() t2+
t2+ ![]() t+6﹣d,PH=t,OA=3,得到
t+6﹣d,PH=t,OA=3,得到 ![]() ,列出方程即可解决问题.(3)首先求出直线AM的解析式,利用方程组求得点M的坐标,分两种情形讨论①如图3中,将线段MA绕点M顺时针旋转90°得到线段MG,过点A作y轴的平行线,过点M作x轴的平行线,两直线交于点E,作GD⊥EM交EM的延长线于D.易知△AME≌△MGD,推出AE=DM=4,EM=DG=8,推出G(9,4),取线段AG的中点T(3,2),作直线MT交抛物线于N1 , 此时∠AMN1=45°,求出直线MT的解析式利用方程组求出交点N的坐标.②设点G关于直线AM的对称点为G1 , 则G1(1,﹣12),取AG1的中点T1 , 作直线MT1交抛物线于N2 , 则∠N2MA=45°,求出直线MT1的解析式,利用方程组即可求出点N1的坐标.
,列出方程即可解决问题.(3)首先求出直线AM的解析式,利用方程组求得点M的坐标,分两种情形讨论①如图3中,将线段MA绕点M顺时针旋转90°得到线段MG,过点A作y轴的平行线,过点M作x轴的平行线,两直线交于点E,作GD⊥EM交EM的延长线于D.易知△AME≌△MGD,推出AE=DM=4,EM=DG=8,推出G(9,4),取线段AG的中点T(3,2),作直线MT交抛物线于N1 , 此时∠AMN1=45°,求出直线MT的解析式利用方程组求出交点N的坐标.②设点G关于直线AM的对称点为G1 , 则G1(1,﹣12),取AG1的中点T1 , 作直线MT1交抛物线于N2 , 则∠N2MA=45°,求出直线MT1的解析式,利用方程组即可求出点N1的坐标.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.