题目内容
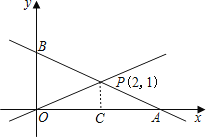
【题目】如图函数y1=kx+b的图象与y2=mx的图象交于点P(2,1),点P是线段AB中点,与x轴正半轴交于点A与y轴交于点 B.
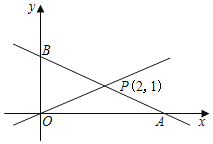
(1)A点坐标是 ,b= ;
(2)根据图象解答:
①解方程组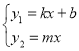
②解不等式组![]()
【答案】(1)(4,0),2;(2)①![]() ;②2<x<4
;②2<x<4
【解析】
(1)如图(见解析),根据中位线的判定与性质得出点C为OA中点,从而可得出OA、OB的长,即可得出答案;
(2)①根据两个一次函数的图象的交点即可得;
②不等式组中的第一个不等式为![]() ,即
,即![]() 的图象位于
的图象位于![]() 的图象的下方,第二个不等式为
的图象的下方,第二个不等式为![]() ,即
,即![]() 的图象位于x轴的上方,找出相应的x的取值范围,由此即可得不等式组的解集.
的图象位于x轴的上方,找出相应的x的取值范围,由此即可得不等式组的解集.
(1)过P作![]() 轴于C
轴于C
∴![]() 轴
轴
∵点P为AB的中点
∴点C为OA中点
![]() 为
为![]() 的中位线,且
的中位线,且![]()
![]()
![]()
∴![]()
∴A点的坐标是![]() ,B点的坐标是
,B点的坐标是![]()
将点B坐标![]() 代入函数
代入函数![]() 得:
得:![]()
故答案为:![]() ,2;
,2;
(2)①∵函数![]() 的图象与
的图象与![]() 的图象交于点
的图象交于点![]()
∴方程组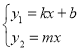 的解是
的解是![]() ;
;
②函数![]() 的图象与
的图象与![]() 的图象交于点
的图象交于点![]() ,
,![]() 与x轴的交点A的坐标是
与x轴的交点A的坐标是![]()
对于不等式组![]()
第一个不等式为![]() ,即
,即![]() 的图象位于
的图象位于![]() 的图象的下方,则
的图象的下方,则![]()
第二个不等式为![]() ,即
,即![]() 的图象位于x轴的上方,则
的图象位于x轴的上方,则![]()
故此不等式组的解集为![]() .
.

练习册系列答案
相关题目