题目内容
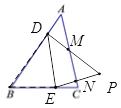
【题目】如图，在△ABC中，AB=7，AC=6，∠A=45°，点D、E分别在边AB、BC上，将△BDE沿着DE所在直线翻折，点B落在点P处，PD、PE分别交边AC于点M、N，如果AD=2，PD⊥AB，垂足为点D，那么MN的长是_____．
【答案】
【解析】∵∠A=45°，∠ADM=90°，∴∠AMD=45°=∠A，
∴DM=AD=2，
∵AB=7，∴BD=7-AD=5，
∵△BDE沿着DE所在直线翻折得到△PDE，
∴PD=BD=5，∠PDE=∠BDE，∴PM=PD-DM=3，
∵∠PDE+∠BDE=∠BDP=90°，
∴∠BDE=45°=∠A，
∴DE//AC，
∴△BDE∽△BAC，
∴BD：BA=DE：AC，
即5：7=DE：6，
∴DE=
，
∵DE//AC，∴△PMN∽△PDE，
∴MN：DE=PM：PD，
即：MN： 
=3：5，
∴MN=
，
故答案为： 
.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
