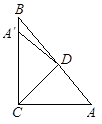题目内容
如图所示，已知在△ABC中，D是BC边上一点，∠1＝∠B，∠2＝∠C，∠BAC＝75°，则∠DAC＝_______°.
40°
试题分析：设∠DAC＝x°，由∠2＝∠C根据三角形的内角和定理可得∠2＝∠C＝
，再根据三角形的外角的性质结合∠1＝∠B可得∠1＝
，最后根据∠BAC＝75°即可列方程求解.设∠DAC＝x°
∵∠2＝∠C
∴∠2＝∠C＝
∴∠1＝∠B＝
∵∠BAC＝75°
∴
，解得
则∠DAC＝40°.
点评：解题的关键是熟练掌握三角形的外角的性质：三角形的一个外角等于与它不相邻的两个内角的和.
练习册系列答案
相关题目
，
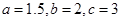
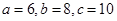
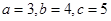
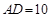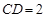，则
的长度可以是（ ）
