题目内容

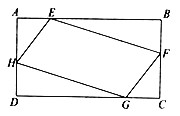
【题目】如图，在矩形中，，点分别在平行四边形各边上，且AE=CG，BF=DH， 四边形的周长的最小值为______．

【答案】20

【解析】

作点E关于BC的对称点E′，连接E′G交BC于点F，此时四边形EFGH周长取最小值，过点G作GG′⊥AB于点G′，由对称结合矩形的性质可知：E′G′=AB，GG′=AD，利用勾股定理即可求出E′G的长度，进而可得出四边形EFGH周长的最小值

作点E关于BC的对称点E′，连接E′G交BC于点F，此时四边形EFGH周长取最小值，EF=E'F，过点G作GG′⊥AB于点G′，如图所示

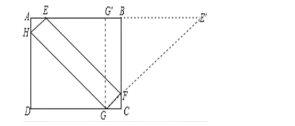
AE=CG. BE=BE′

E′G′=AB=8,

GG′=AD=6

E`G=

∵C四边形EFGH=2(GF+EF)=2E′G=20

练习册系列答案
相关题目

【题目】如图，直线y=-2x+6与x轴交于点A，与直线y=x交于点B.

(1)点A坐标为_____________.

(2)动点M从原点O出发，以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动，过点M作MP⊥x轴交直线y=x于点P，然后以MP为直角边向右作等腰直角△MPN.设运动t秒时，ΔMPN与ΔOAB重叠部分的面积为S.求S与t之间的函数关系式，并直接写出t的取值范围.

【题目】请阅读下列材料：

问题：如图1,△ABC中,∠ACB=90°,AC=BC,MN是过点A的直线,DB⊥MN于点D,联结CD.求证：BD+AD= CD.

小明的思考过程如下：要证BD+AD=CD,需要将BD,AD转化到同一条直线上,可以在MN上截取AE=BD,并联结EC,可证△ACE和△BCD全等,得到CE=CD,且∠ACE=∠BCD,由此推出△CDE为等腰直角三角形,可知DE=CD，于是结论得证。

小聪的思考过程如下：要证BD+AD=CD,需要构造以CD为腰的等腰直角三角形,可以过点C作CE⊥CD交MN于点E,可证△ACE和△BCD全等,得到CE=CD,且AE=BD,由此推出△CDE为等腰直角三角形,可知DE=CD，于是结论得证。

请你参考小明或小聪的思考过程解决下面的问题：

(1)将图1中的直线MN绕点A旋转到图2和图3的两种位置时，其它条件不变，猜想BD，AD，CD之间的数量关系，并选择其中一个图形加以证明；

(2)在直线MN绕点A旋转的过程中,当∠BCD=30°,BD=时，CD=___.

【题目】已知：如图，点C是线段AB上一点，且3AC＝2AB．D是AB的中点，E是CB的中点，DE＝6，求：

（1）AB的长；

（2）求AD：CB．

【题目】在平面直角坐标系中，点A、B分别在x轴、y轴上，点A与点C关于y轴对称，点E是线段AC上的点（点E不与点A、C重合）

（1）若点A的坐标为（a，0），则点C的坐标为 ；

（2）如图1，点F是线段AB上的点，若∠BEF=∠BAO，∠BAO=2∠OBE，求证：AF=CE；

（3）如图2，若点D为AC上一点，连接ED，满足BE=BD，试探究∠ABE与∠DEC的关系．

【题目】如图，在△ABC中，已知AB=AC=10cm，BC=16cm，AD⊥BC于D，点E、F分别从B、C两点同时出发，其中点E沿BC向终点C运动，速度为4cm/s；点F沿CA、AB向终点B运动，速度为5cm/s，设它们运动的时间为x（s）．

（1）求x为何值时，△EFC和△ACD相似；

（2）是否存在某一时刻，使得△EFD被 AD分得的两部分面积之比为3:5，若存在，求出x的值，若不存在，请说明理由；

（3）若以EF为直径的圆与线段AC只有一个公共点，求出相应x的取值范围．

【题目】如图,直线y=x+与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0)，⊙P与y轴相切于点O.若将⊙P沿x轴向左平移，当⊙P与该直线相切时，点P坐标为___.

【题目】如图所示，已知∠BAC=∠EAD=90o.

（1）判断∠BAE与∠CAD的大小关系，并说明理由.

（2）当∠EAC=60o时，求∠BAD的大小.

（3）探究∠EAC与∠BAD的数量关系，请直接写出结果,不要求说明理由.

【题目】如图是由7个同样大小棱长为1的小正方体搭成的几何体，请分别画出它的主视图、左视图和俯视图.

（2）这个组合几何体的表面积为　 　个平方单位（包括底面积）；

（3）用小立方体搭一几何体，使得它的俯视图和左视图与你在上图方格中所画的图一致，则搭这样的几何体最多要________个小立方体.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网