题目内容
【题目】请阅读下列材料：
问题：如图1,△ABC中,∠ACB=90°,AC=BC,MN是过点A的直线,DB⊥MN于点D,联结CD.求证：BD+AD=
CD.
小明的思考过程如下：要证BD+AD=CD,需要将BD,AD转化到同一条直线上,可以在MN上截取AE=BD,并联结EC,可证△ACE和△BCD全等,得到CE=CD,且∠ACE=∠BCD,由此推出△CDE为等腰直角三角形,可知DE=CD，于是结论得证。
小聪的思考过程如下：要证BD+AD=CD,需要构造以CD为腰的等腰直角三角形,可以过点C作CE⊥CD交MN于点E,可证△ACE和△BCD全等,得到CE=CD,且AE=BD,由此推出△CDE为等腰直角三角形,可知DE=CD，于是结论得证。
请你参考小明或小聪的思考过程解决下面的问题：
(1)将图1中的直线MN绕点A旋转到图2和图3的两种位置时，其它条件不变，猜想BD，AD，CD之间的数量关系，并选择其中一个图形加以证明；
(2)在直线MN绕点A旋转的过程中,当∠BCD=30°,BD=时，CD=___.
【答案】（1）BDAD=
CD.，证明见解析；（2）
±1.
【解析】
（1）过点C作CE⊥CB于点C，与MN交于点E，证明△ACE≌△DCB，则△ECB为等腰直角三角形，据此即可得到BE=CB，根据BE=AB-AE即可证得；
（2）过点B作BH⊥CD于点H，证明△BDH是等腰直角三角形，求得DH的长，在直角△BCH中，利用直角三角形中30°的锐角所对的直角边等于斜边的一半，即可求得．
（1）如图2,过点C作CE⊥CD交MN于点E,则∠2=90°.
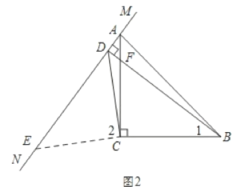
∵∠ACB=90°，∴∠2+∠ACD=∠ACB+∠ACD，
即∠ACE=∠BCD.
设AC与BD相交于点F,∵DB⊥MN,∴∠ADB=90°.
∴∠CAE+∠AFD=90°,∠1+∠BFC=90°.
∵∠AFD=∠BFC，∴∠CAE=∠1.
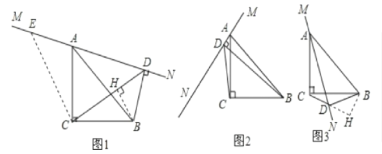
在△ACE和△BCD中
，
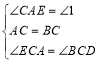∴△ACE≌△BCD(ASA).
∴CE=CD，AE=BD.
在Rt△CDE中,∵CD
+CE=DE，
∴2CD=DE,即DE=CD.
∵DE=AEAD=BDAD,∴BDAD=CD.
(2)MN在绕点A旋转过程中，这个的意思并没有指明是哪种情况，
∴综合了第一个图和第二个图两种情况
若是第1个图：易证△ACE≌△DCB，CE=CD，
∴△ECD为等腰直角三角形，
∴∠AEC=45°=∠CBD，
过D作DH⊥CB.则△DHB为等腰直角三角形。
BD=BH，
∴BH=DH=1
直角三角形△CDH中，
∠DCH=30°，
BH=1,则CH= .
∴CD=+1
若是第二个图：过B作BH⊥CD交CD延长于H.
解法类似上面,CH=,DH=1,CD=1.
故答案为：±1.
