题目内容
【题目】如图,直线y=![]() x+
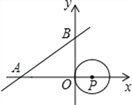
x+![]() 与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.
与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.
【答案】(-1,0),(-5,0);
【解析】分析:画出⊙P与直线AB相切时的图形,计算出AB与x轴的夹角,结合勾股定理和含30°角的直角的性质求AP1,AP2的长.
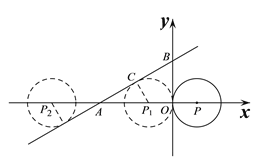
详解:如图,当圆心P运动到点P1,P2时,与直线AB相切.
当y=0时,![]() x+
x+![]() =0,解得x=-3,所以A(-3,0);
=0,解得x=-3,所以A(-3,0);
当x=0时,y=![]() ,所以B(0,
,所以B(0,![]() ).
).
Rt△ABO中,则勾股定理得AB=6,所以∠BAO=30°.
因为AB与⊙P1相切,所以∠ACP1=90°,所以AP1=2P1C=2.
所以OP1=3-2=1,则P1(-1,0).
同理AP2=2,则OP2=3+2=5,则P2(-5,0).
故答案为(-1,0),(-5,0).

练习册系列答案
相关题目