Question

【题目】在平面直角坐标系中，点A、B分别在x轴、y轴上，点A与点C关于y轴对称，点E是线段AC上的点（点E不与点A、C重合）

（1）若点A的坐标为（a，0），则点C的坐标为 ；

（2）如图1，点F是线段AB上的点，若∠BEF=∠BAO，∠BAO=2∠OBE，求证：AF=CE；

（3）如图2，若点D为AC上一点，连接ED，满足BE=BD，试探究∠ABE与∠DEC的关系．

Answer 1

【答案】（1）（-a，0）．（2）证明见解析；（3）∠ABE=2∠DEC．

【解析】

（1）利用对称性直接写成点C的坐标；

（2）根据三角形的内角和，等腰三角形的性质先判断出，∠ABE=∠BFE，进而得出BE=EF，在判断出，∠CBE=∠AEF，进而判定，△AEF≌△CBE，即可得出结论；

（3）设∠OBE=α，∠CBE=β，用三角形的内角和表示出∠ABE=2α+β，利用等腰三角形的性质表示出∠DEC=（2α+β），即可得出结论．

（1）∵点A（a，0）与点C关于y轴对称，

∴C（-a，0），

故答案为（-a，0）．

（2）设∠OBE=α，

∴∠BAO=2∠OBE=2α，∠BEF=∠BAO=α，

由对称得，OA=OC，

∵BO⊥AC，

∴AB=CB，

∴∠BAO=∠BCO=2α，

∴∠ABE=∠ABO+∠OBE=90°-α，

在△BEF中，∠BFE=180°-（∠BEF+∠EBF）=90°-α，

∴∠ABE=∠BFE，

∴BE=EF，

在Rt△AOB中，∠ABO=90°-2α，

∴∠ACB=2α，∠CBO=∠90°-2α，

∵∠OBE=α，

∴∠CBE=90°-3α，

在△BCE中，根据三角形的内角和得，∠BEC=90°+α，

∴∠AEF=180°-∠BEF-∠BEC=90°-3α，

∴∠CBE=∠AEF，

在△AEF和△CBE中，，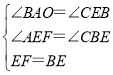

∴△AEF≌△CBE，

∴AF=CE，

（3）设∠OBE=α，∠CBE=β，

∴∠CBO=α+β，由（1）知，∠ABO=∠CBO=α+β，

∴∠ABE=∠ABO+∠OBE=α+β+α=2α+β，

在Rt△OBE中，∠OEB=90°-α，

在△BDE中，BD=BE，

∴∠BED=90°-β，

∴∠DEC=180°-∠OEB-∠BED=（2α+β），

∵∠ABE=2α+β，

∴∠ABE=2∠DEC．