题目内容
【题目】如图,直线y=-2x+6与x轴交于点A,与直线y=x交于点B.
(1)点A坐标为_____________.
(2)动点M从原点O出发,以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动,过点M作MP⊥x轴交直线y=x于点P,然后以MP为直角边向右作等腰直角△MPN.设运动t秒时,ΔMPN与ΔOAB重叠部分的面积为S.求S与t之间的函数关系式,并直接写出t的取值范围.

【答案】(1)(3,0);(2)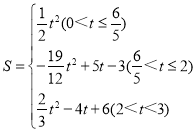
【解析】
(1)将y=0代入y=-2x+6可得x=3,即可得出点A坐标;
(2)分点N在直线AB左侧时,点N在直线AB右侧且P在直线AB左侧时,以及点P在直线AB右侧三种情况讨论,利用数形结合的思想,根据重叠部分的形状,分别用含t的式子表示出三角形的底边和高,从而得到重叠部分的面积.
(1) 将y=0代入y=-2x+6可得x=3,
所以点A坐标为(3,0)
故答案为:(3,0)
(2)如图一,
由![]() 得
得![]()

∴B(2,2)
过点B作BH⊥x轴于点H
∴BH=OH=2,∠AOB=45°
∵PM⊥x轴
∴OM=MP=t
∵等腰直角ΔMPN
∴PN∥x轴
∴∠N=∠NMA=45°
∴∠AOB=∠NMA=45°
∴MN∥OB
∴设直线MN为y=x+b
∵OM=t
∴y=x-t
当点N在直线y=-2x+6上时,OM=PM=PN=t,
∴N(2t,t)
∴t=-2×2t+6,解得:t=![]()
∴当![]() 时,
时,![]()
如图二,当点P在直线y=-2x+6上时,OM=PM=t,
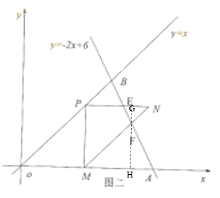
可得t=-2t+6,解得:t=2
当![]() 时,PN与AB交于点E,MN与AB交于点F,
时,PN与AB交于点E,MN与AB交于点F,
∵P(t,t)
∴t=-2x+6
∴![]()
∴![]()
∴![]()
∴![]()
∵OA=3
∴MA=3-t
由![]()
得F(2+![]() t,2-
t,2-![]() t)
t)
过点F作△ENF的高GF, △FMA的高HF
∴HF=2-![]() t
t
∴![]()
∴![]()
∴![]() ;
;
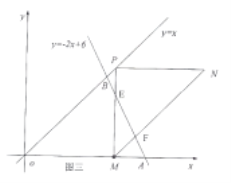
如图三,当M与A重合时,t=3
故当![]() 时,PM与AB交于点E,MN与AB交于点F,有E(t, -2t+6),F(2+
时,PM与AB交于点E,MN与AB交于点F,有E(t, -2t+6),F(2+![]() t,2-
t,2-![]() t),
t),
∴![]() ,
,
∴![]() ;
;
综上所述,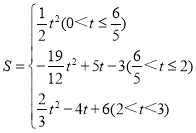 .
.