题目内容
【题目】某商店出售一款商品,经市场调查反映,该商品的日销售量y(件)与销售单价x(元)之间满足一次函数关系,关于该商品的销售单价,日销售量,日销售利润的部分对应数据如表:[注:日销售利润=日销售量×(销售单价﹣成本单价)
销售单价x(元) | 75 | 78 | 82 |
日销售量y(件) | 150 | 120 | 80 |
日销售利润w(元) | 5250 | a | 3360 |
(1)根据以上信息,填空:该产品的成本单价是 元,表中a的值是 ,y关于x的函数关系式是 ;
(2)求该商品日销售利润的最大值.
(3)由于某种原因,该商品进价降低了m元/件(m>0),该商店在今后的销售中,商店规定该商品的销售单价不低于68元,日销售量与销售单价仍然满足(1)中的函数关系,若日销售最大利润是6600元,直接写出m的值.
【答案】(1)40、4560、y=﹣10x+900;(2)6250;(3)m的值为2.
【解析】
(1)根据日销售利润=日销售量×(销售单价﹣成本单价)即可求解;
(2)根据二次函数的顶点式即可求解;
(3)根据日销售利润=日销售量×(销售单价﹣成本单价),把销售的最大利润代入即可求解.
(1)设该产品的成本单价是n元,根据题意,得
5250=150×(75﹣n),解得n=40.
a=120×(78﹣40)=4560.
设日销售量y(件)与销售单价x(元)之间满足的一次函数解析式为y=kx+b,
把(75,150),(78,120)代入得:![]() , 解得:
, 解得:![]()
一次函数解析式为y=﹣10x+900.
故答案为40、4560、y=﹣10x+900.
(2)根据题意,得
w=(x﹣40)(﹣10x+900)
=﹣10x2+1300x﹣36000
=﹣10(x﹣65)2+6250.
答:该商品日销售利润的最大值为6250元.
(3)∵销售单价不低于68元,日销售量与销售单价仍然满足(1)中的函数关系,
日销售最大利润是6600元时,即当x=68时,最大利润为6600元.
设商品降低后的进价为a元,根据题意,得
(﹣10×68+900)(68﹣a)=6600,
解得a=38,
∴m=40﹣38=2.
答:m的值为2.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
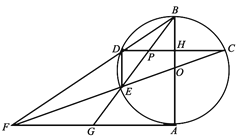
开心蛙口算题卡系列答案【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,且恰好
,且恰好![]() ∥
∥![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)求证:点![]() 是
是![]() 的中点;
的中点;
(3)当⊙![]() 的半径为
的半径为![]() 时,求
时,求![]() 的值.
的值.
【题目】期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
(收集数据)
(1)若要从全年级学生中抽取一个48人的样本,你认为以下抽样方法中比较合理的有 ;(只要填写序号即可)
①随机抽取一个班级的48名学生;②在全年级学生中随机抽取48名学生;③在全年级12个班中分别各抽取4名学生;④从全年级学生中随机抽取48名男生;
(整理数据)
(2)将抽取的48名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图(不完整)如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 、
②估计全年级A、B类学生大约一共有 名;

成绩(分) | 频数 | 频率 |
A类(80~100) | 0.5 | |
B类(60~79) | 0.25 | |
C类(40~59) | 8 | |
D类(0~39) | 4 |
(3)学校为了解其他学校教学情况,将同层次的第一、第二两所中学的抽样数据进行对比,得下表:
学校 | 平均分(分) | 极差(分) | 方差 | A、B类的频率和 |
第一中学 | 71 | 52 | 432 | 0.75 |
第二中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校的教学效果较好?结合数据,请给出一个解释来支持你的观点.