题目内容
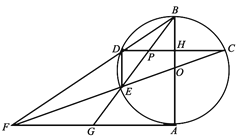
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,且恰好
,且恰好![]() ∥
∥![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)求证:点![]() 是
是![]() 的中点;
的中点;
(3)当⊙![]() 的半径为
的半径为![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() =
=![]() .
.
【解析】
(1)根据![]() ∥
∥![]() ,
,![]() 可证FA⊥AB,则可得
可证FA⊥AB,则可得![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)连接![]() ,易证△GEA∽△GAB,可得
,易证△GEA∽△GAB,可得![]() ,根据
,根据![]() ∥
∥![]() ,可得
,可得![]() ,即有
,即有![]() ,可证点
,可证点![]() 是
是![]() 的中点;
的中点;
(3)利用![]() ∥
∥![]() ,得:
,得:![]() ,易证DE=BH,根据点O是CE中点,点H是CD的中点,得
,易证DE=BH,根据点O是CE中点,点H是CD的中点,得![]() ,有OH=2,CH=
,有OH=2,CH=![]() ,可求得
,可求得![]() =tan∠OCH =
=tan∠OCH =![]() .
.
(1)证明:∵![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]()
∴AB⊥CD,又![]() ∥
∥![]() ,
,
∴FA⊥AB,
∴![]() 是⊙
是⊙![]() 的切线.
的切线.
(2)证明:连接![]() ,
,

∵![]() 是⊙
是⊙![]() 的直径,
的直径,
∴AE⊥BG.又FA⊥AB,
∴∠GEA=∠GAB,
又∵∠GBA=∠ABG.
∴△GEA∽△GAB,
∴![]()
![]()
∵![]() ∥
∥![]() ,
,
∴∠C=∠EFG,又∠C=∠FBE.
∴∠EFG=∠FBG,又∠FGE=∠BGF.
∴△EFG∽△FBG,
∴![]()
![]()
![]() ,
,
![]()
∴点![]() 是
是![]() 的中点;
的中点;
(3)解:∵![]() ∥
∥![]() ,∴
,∴![]() .
.
又∵GF=GA,∴DP=HP.
又∵CE是⊙![]() 的直径,D在圆上∴CD⊥DE,
的直径,D在圆上∴CD⊥DE,
又∵AB⊥CD于点H,
∴点H是CD的中点,AB∥DE,
又∵DP=HP,
∴DE=BH,
又∵点O是CE中点,点H是CD的中点,
∴![]()
又∵⊙![]() 的半径为6,
的半径为6,
∴OH=2,CH=![]() ,
,
∴![]() =tan∠OCH =
=tan∠OCH =![]()

【题目】苏北五市联合通过网络投票选出了一批“最有孝心的美少年”.根据各市的入选结果制作出如下统计表,后来发现,统计表中前三行的所有数据都是正确的,后两行中有一个数据是错误的.请回答下列问题:
(1)统计表![]() ________,
________,![]() ________;
________;
(2)统计表后三行中哪一个数据是错误的?该数据的正确值是多少?
(3)组委会决定从来自宿迁市的4位“最有孝心的美少年”中,任选两位作为苏北五市形象代言人,![]() 、
、![]() 是宿迁市“最有孝心的美少年”中的两位,问
是宿迁市“最有孝心的美少年”中的两位,问![]() 、
、![]() 同时入选的概率是多少?并请画出树状图或列出表格.
同时入选的概率是多少?并请画出树状图或列出表格.
区域 | 频数 | 频率 |
宿迁 | 4 | a |
连云港 | 7 | 0.175 |
淮安 |
| 0.2 |
徐州 | 10 | 0.25 |
盐城 | 12 | 0.275 |
【题目】某旅行团计划今年暑假组织一个老年人团去昆明旅游,预定宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准为每人每天120元,并且各自推出不同的优惠方案.甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.设老年团的人数为![]() .
.
(1)根据题意,用含有![]() 的式子填写下表:
的式子填写下表:
|
|
|
| |
甲宾馆收费/元 |
| 5280 | ||
乙宾馆收费/元 |
|
| 5400 |
(2)当老年人团的人数为何值时,在甲、乙两家宾馆的花费相同?如果老年人团的人数超过60人,在哪家宾馆住宿比较省钱?