题目内容
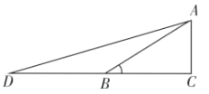
【题目】如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点;
(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.
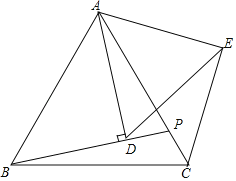
【答案】(1)见解析;(2)见解析;(3)1
【解析】
(1)由等边三角形的性质和旋转的性质可得∠DAB=∠CAE,AB=AC,AD=AE,即可证△ADB≌△AEC,可得BD=CE;
(2)过点C作CG//BP,交EF的延长线于点G,由等边三角形的性质和全等三角形的性质可得CG=BD,∠BDG=∠G,∠BFD=∠GFC,可证△BFD≌△CFG,可得结论;
(3)由题意可证点A,点F,点C,点E四点在以AC为直径的圆上,由直径是圆的最大弦可得EF的最大值.
证明:(1)∵将线段AD绕点A逆时针旋转60°得到线段AE
∴AD=AE,∠DAE=60°
∴△ADE是等边三角形
∵△ABC为等边三角形
∴AB=AC, ∠BAC=∠DAE=60°
∴∠DAB=∠CAE,且AB=AC,AD=AE
∴△ADB≌△AEC(SAS)
∴BD=CE
(2)如图,过点C作CG∥BP,交EF的延长线于点G
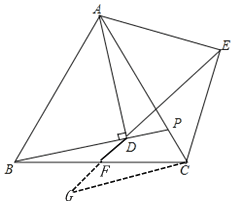
∵∠ADB=90°, ∠ADE=60°
∴∠BDG=30°
∵CG∥BP
∴∠G=∠BDG=30°
∵△ADB≌△AEC
∴BD=CE,∠ADB=∠AEC=90°
∴∠GEC=∠AEC﹣∠AED=30°
∴∠G=∠GEC=30°
∴GC=CE
∴CG=BD,且∠BDG=∠G, ∠BFD=∠GFC
∴△BFD≌△CFG(AAS)
∴BF=FC
∴点F是BC中点
(3)如图,连接AF,
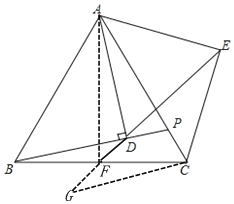
∵△ABC是等边三角形,BF=FC
∴AF⊥BC
∴∠AFC=90°
∴∠AFC=∠AEC=90°
∴点A,点F,点C,点E四点在以AC为直径的圆上
∴EF最大为直径,
即最大值为1

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案