Question

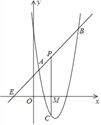
【题目】如图（1），一平面直角坐标第xOy中，直线与y轴相交于点A，与反比例函数（x>0)的图像相交于点B（m,2)

（1）求反比例函数的表达式；

（2）若将直线向上平移4个单位长度后与y轴交于点C，求ΔABC的面积；

（3）如图（2）将直线向上平移，与反比例函数的图像交于点D，连接DA,DB.若

ΔABC的面积为3，求平移后直线的表达式。

图（1） 图（2）

Answer 1

【答案】（1）反比例函数的关系式是；（2）ΔABC的面积等于3；（3）平移后直线的表达式为

【解析】试题分析：（1）先根据直线y=2x-1经过点B（m，2），求得B（1.5，2），再根据反比例函数y= （x＞0）的图象经过点B，即可得到k的值；
（2）过B作BH⊥y轴于H，根据AC=4，BH=1.5，即可得到△ABC的面积；
（3）设直线y=2x-1向上平移后与y轴交于点E，连接BE，过B作BM⊥y轴于M，则BM=1.5，根据DE∥AB，可得S△ABE=S△ABD=3，进而得到AE=4，再根据OA=1，可得OE=3，即可得出平移后直线的表达式为y=2x+3．

试题解析：

（1）∵直线经过点B（m,2)

∴,解得，∴点B的坐标是（）

∵反比例函数的图象经过点B(),∴

∴反比例函数的关系式是

（2）过点B作BH⊥y轴于点H

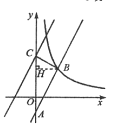
根据题意，得AC=4

由（1），得点B的坐标为（）

∴,

∴

∴ΔABC的面积等于3

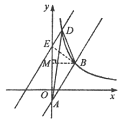
（3）设直线向上平移后与y轴交于点E，连接BE,过点B作

BM⊥y轴于点M，则。

∵DE∥AB,ΔABD的面积为3.

∴

∴,即，

∴AE=4。

∵OA=1,

∴OE=3

∴平移后直线的表达式为