题目内容
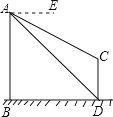
【题目】如图△ABC中，点D是边AB的中点，CE∥AB，且AB=2CE，连结BE、CD。
（1）求证：四边形BECD是平行四边形；
（2）用无刻度的直尺画出△ABC边BC上的中线AG(保留画图痕迹)
【答案】（1）证明见解析 （2）答案见解析
【解析】
（1）利用线段中点的定义可证得AB=2BD，再结合已知证明BD=CE，然后利用有一组对边平行且相等的四边形是平行四边形，可得结论；
（2）连接DE交BC于点G ，连接AG，利用平行四边形的对角线互相平分，可得点G时BC的中点，利用三角形的中线的定义，可知AG是中线.
（1）解： ∵点D是边AB的中点，
∴AB=2BD，
∵AB=2CE，
∴BD=CE；
∵CE∥AB
∴四边形BECD是平行四边形。
（2）解： 连接DE交BC于点G ，连接AG，
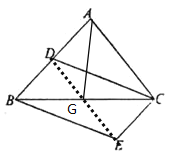
∵四边形BECD是平行四边形，
∴BG=CG，
∴AG是△ABC的BC边上的中线，
即AG就是所求作的图形.
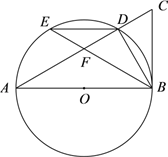
【题目】如图，AB为⊙O的直径，点D，E为⊙O上的两个点，延长AD至C，使∠CBD=∠BED.
（1）求证：BC是⊙O的切线；
（2）当点E为弧AD的中点且∠BED=30°时，⊙O半径为2，求DF的长度.
【题目】王达和李力是八(2)班运动素质最好的两位同学，为了选出一名同学参加全校的体育运动大寒，班主任针对学校要测试的五个项目，对两位同学进行相应的测试(成绩：分)，结果如下：
姓名 | 力量 | 速度 | 耐力 | 柔韧 | 灵敏 |
王达 | 60 | 75 | 100 | 90 | 75 |
李力 | 70 | 90 | 80 | 80 | 80 |
根据以上测试结果解答下列问题：
（1）补充完成下表：
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差(分2) |
王达 | 80 | 75 | 75 | 190 |
李力 |
（2）任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由；
（3）若按力量：速度：耐力：柔韧：灵敏=1：2：3：3：1的比例折合成综合分数，推选得分同学参加比赛，请通过计算说明应推选哪位同学去参赛。
【题目】用A4纸复印文件，在甲复印店不管一次复印多少页，每页收费0.1元.在乙复印店复印同样的文件，一次复印页数不超过20时，每页收费0.12元；一次复印页数超过20时，超过部分每页收费0.09元.设在同一家复印店一次复印文件的页数为
（为非负整数）.
（1）根据题意，填写下表：
一次复印页数（页） | 5 | 10 | 20 | 30 | … |
甲复印店收费（元） |
| 2 | … | ||
乙复印店收费（元） |
|
| … |
（2）设在甲复印店复印收费
元，在乙复印店复印收费
元，分别写出
关于的函数关系式；
（3）当
时，顾客在哪家复印店复印花费少？请说明理由.
