Question

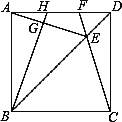
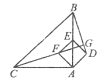
【题目】如图，在RtΔABC中，AB=AC=4,∠BAC=900.点E为AB的中点，以AE为对角线作正方形ADEF，连接CF并延长交BD于点G，则线段CG的长等于________________.

Answer 1

【答案】

【解析】延长AF交BC于M，AB交CG于O．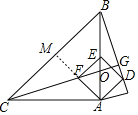

∵AB=AC=4，∠CAB=90°，
∴BC=

∵AE=EB=2，四边形AFED是正方形，
∴AF=EF=

，∴∠EAF=∠EAD=45°，
∴∠MAB=∠MAC=45°，
∴CM=BM=AM=2

∴FM=AM-AF=

在Rt△CMF中，CF＝ ＝,

∵AC=AB，∠CAF=∠BAD=45°，AF=AD，
∴△CAF≌△BAD，
∴∠ACF=∠ABD，
∵∠AOC=∠BOG，
∴∠CAO=∠BGO=90°，
∵∠MCF=∠BCG，∠CMF=∠CGB=90°，
∴△CMF∽△CGB，

∴

∴,

∴CG=.

故答案是： .