题目内容
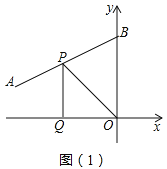
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(![]() ,
,![]() )和B(4,m),点P是AB上的动点,设点P的横坐标为n,过点P作PC⊥x轴,交抛物线于点C,与x轴交于M点.
)和B(4,m),点P是AB上的动点,设点P的横坐标为n,过点P作PC⊥x轴,交抛物线于点C,与x轴交于M点.
(1)求抛物线的表达式;
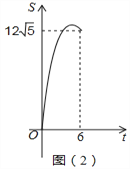
(2)点P是线段AB上异于A,B的动点,是否存在这样的点P,使线段PC的长有最大值?若存在,求出这最大值,若不存在,请说明理由;
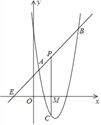
(3)点P在直线AB上自由移动,当三个点C,P,M中恰有一点是其它两点所连线段的中点时,请直接写出m的值.
【答案】(1) y=2x2﹣8x+6;(2)见解析;(3) n的值为![]() 或
或![]() .
.
【解析】分析:(1)把B(4,m)代入y=x+2中求出m得到B(4,6),然后把A点和B点坐标代入y=ax2+bx+6得到关于a、b的方程组,再解方程组即可得到抛物线解析式;
(2)设P的坐标为(n,n+2)(![]() <n<4),则点C的坐标为(n,2n2-8n+6),用n表示PC得到PC=(n+2)-(2n2-8n+6),然后根据二次函数的性质解决问题;
<n<4),则点C的坐标为(n,2n2-8n+6),用n表示PC得到PC=(n+2)-(2n2-8n+6),然后根据二次函数的性质解决问题;
(3)设P的坐标为(n,n+2),则点C的坐标为(n,2n2-8n+6),讨论:若M点为PC的中点,则PM=CM,即n+2=-(2n2-8n+6);若P点为CM的中点,则PM=PC,即2n2-8n+6=2(x+2);若C点为PM的中点,则PC=CM,即n+2=2(2n2-8n+6),然后分别解方程可确定满足条件的n的值.
详解:
(1)∵B(4,m)在直线y=x+2上,
∴m=6,则B(4,6),
∵A(![]() ,
,![]() )、B(4,6)在抛物线y=ax2+bx+6上,
)、B(4,6)在抛物线y=ax2+bx+6上,
∴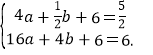 解得
解得![]() ,
,
∴所求抛物线的表达式为y=2x2﹣8x+6;
(2)设P的坐标为(n,n+2)(![]() <n<4),则点C的坐标为(n,2n2﹣8n+6),
<n<4),则点C的坐标为(n,2n2﹣8n+6),
∴PC=(n+2)﹣(2n2﹣8n+6)=﹣2n2+9n﹣4=﹣2(n﹣![]() )2+
)2+![]() ,
,
∵a=﹣2<0,
∴当n=![]() 时,线段PC取得最大值
时,线段PC取得最大值![]() ;
;
(3)设P的坐标为(n,n+2),则点C的坐标为(n,2n2﹣8n+6),
若M点为PC的中点,则PM=CM,即n+2=﹣(2n2﹣8n+6),整理得2n2﹣7n+8=0,此方程没有实数解;
若P点为CM的中点,则PM=PC,即2n2﹣8n+6=2(x+2),整理得n2﹣5n+5=0,解得n1=![]() ,n2=
,n2=![]() ;
;
若C点为PM的中点,则PC=CM,即n+2=2(2n2﹣8n+6),整理得4n2﹣17n+10=0,解得n1=![]() ,n2=
,n2=![]() ;
;
综上所述,n的值为![]() 或
或![]() .
.

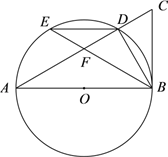
【题目】如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
(1)求证:BC是⊙O的切线;
(2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度.
【题目】王达和李力是八(2)班运动素质最好的两位同学,为了选出一名同学参加全校的体育运动大寒,班主任针对学校要测试的五个项目,对两位同学进行相应的测试(成绩:分),结果如下:
姓名 | 力量 | 速度 | 耐力 | 柔韧 | 灵敏 |
王达 | 60 | 75 | 100 | 90 | 75 |
李力 | 70 | 90 | 80 | 80 | 80 |
根据以上测试结果解答下列问题:
(1)补充完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差(分2) |
王达 | 80 | 75 | 75 | 190 |
李力 |
(2)任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由;
(3)若按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,推选得分同学参加比赛,请通过计算说明应推选哪位同学去参赛。