Question

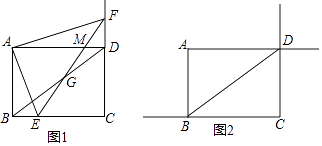
【题目】如图，菱形ABCD内两点M、N，满足MB⊥BC，MD⊥DC，NB⊥BA，ND⊥DA，若四边形BMDN的面积是菱形ABCD面积的 ，则cosA= ．

Answer 1

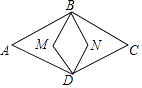
【答案】
【解析】解：如图，连接AN、CM，延长BM交AD于H．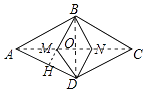
∵AB⊥BN，AD⊥DN，
∴∠ABN=∠ADN=90°，
在Rt△ANB和Rt△AND中，
，
∴△ABN≌△ADN，
∴∠BAN=∠DAN，
∴AN是菱形ABCD的角平分线，同理CM也是菱形ABCD的角平分线，设BD与AC交于点O，
易知四边形BMDN是菱形，设S△OMB=S△ONB=S△OMD=S△OND=a，
∵四边形BMDN的面积是菱形ABCD面积的 ，
∴S△AMB=S△AMD=S△CNB=S△CND=4a，
∴AM=4OM，CN=4ON，设ON=OM=k，则AM=CN=4k，
∵△ABO∽△BNO，
∴OB2=OAON=5k2 ，
∴OB= k，AB=AD= = k，
∵ ADBH= BDAO，
∴BH= = ，
∴AH= = = k，
∴cosA= = = ．
故答案为
如图，连接AN、CM，延长BM交AD于H．AN是菱形ABCD的角平分线，同理CM也是菱形ABCD的角平分线，设BD与AC交于点O，
易知四边形BMDN是菱形，设S△OMB=S△ONB=S△OMD=S△OND=a，因为四边形BMDN的面积是菱形ABCD面积的 ，所以S△AMB=S△AMD=S△CNB=S△CND=4a，推出AM=4OM，CN=4ON，设ON=OM=k，则AM=CN=4k，由△ABO∽△BNO，推出OB2=OAON=5k2 ， 推出OB= k，AB=AD= = k，由 ADBH= BDAO，推出BH= = ，再利用勾股定理求出AH即可解决问题．