题目内容
【题目】平面直角坐标系xOy中，对称轴平行于y轴的抛物线过点A（1，0）、B（3，0）和C（4，6）；
（1）求抛物线的表达式；
（2）现将此抛物线先沿x轴方向向右平移6个单位，再沿y轴方向平移k个单位，若所得抛物线与x轴交于点D、E（点D在点E的左边），且使△ACD∽△AEC（顶点A、C、D依次对应顶点A、E、C），试求k的值，并注明方向．
【答案】
（1）
解：∵抛物线过点A（1，0）、B（3，0），
∴设抛物线的解析式为y=a（x﹣1）（x﹣3），
∵C（4，6），
∴6=a（4﹣1）（4﹣3），
∴a=2，
∴抛物线的解析式为y=2（x﹣1）（x﹣3）=2x2﹣8x+6
（2）
解：如图，
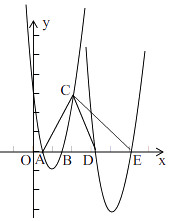
设点D（m，0），E（n，0），
∵A（1，0），
∴AD=m﹣1，AE=n﹣1
由（1）知，抛物线的解析式为y=2x2﹣8x+6=2（x﹣2）2﹣2；
∴将此抛物线先沿x轴方向向右平移6个单位，得到抛物线的解析式为y=2（x﹣8）2﹣2；
∴再沿y轴方向平移k个单位，得到的抛物线的解析式为y=2（x﹣8）2﹣2﹣k；
令y=0，则2（x﹣8）2﹣2﹣k=0，
∴2x2﹣32x+126﹣k=0，
根据根与系数的关系得，
∴m+n=16，mn=63﹣ 
，
∵A（1，0），C（4，6），
∴AC2=（4﹣1）2+62=45，
∵△ACD∽△AEC，
∴ 
，
∴AC2=ADAE，
∴45=（m﹣1）（n﹣1）=mn﹣（m+n）+1，
∴45=63﹣ ﹣16+1，
∴k=6，
即：k=6，向下平移6个单位．
【解析】（1）利用待定系数法直接求出抛物线的解析式；（2）设出D，E坐标，根据平移，用k表示出平移后的抛物线解析式，利用坐标轴上点的特点得出m+n=16，mn=63﹣ ，进而利用相似三角形得出比例式建立方程即可求出k
【考点精析】关于本题考查的二次函数的图象和二次函数图象以及系数a、b、c的关系，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）才能得出正确答案．
